Конечных разностей исчисление

КОНЕЧНЫХ РАЗНОСТЕЙ ИСЧИСЛЕНИЕ, раздел математики, в котором изучаются связи между функциями и разностями их значений (или линейными комбинациями таких значений) в заранее выбранных точках. Прямой разностью 1-го порядка с шагом h функции f(x) в точке х называется величина

Δ¹_h[f] (x)  = f (x+h) -f(x),

обратной разностью - величина

Δ¹_h[f] (x) = f(x)-f(x-h),

центральной разностью - величина

δ¹_h[f] (x) = f(x+h/2) - f(x - h/2).

Прямые разности более высоких порядков определяются индуктивно по формулам

Δⁿ⁺¹_h[f] (x) = Δ¹_h[Δⁿ_h[f] (x), n = 1, 2 и аналогично для других разностей. Справедливы равенства

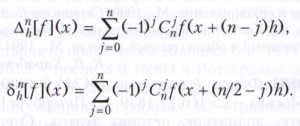
Для дифференцируемых функций с помощью конечных разностей n-го порядка при малых значениях h можно получить приближения производных n-го порядка. Точность приближения производных функции f её конечными разностями при h → 0 зависит как от свойств функции f, так и от вида разности, например:

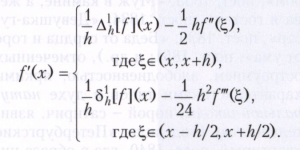
При численном решении дифференциальных уравнений входящие в эти уравнения производные заменяют конечными разностями, что приводит к системе рекуррентных уравнений (смотри Рекуррентные соотношения) относительно значений искомой функции в точках, образующих некоторую арифметическую прогрессию. Точность такого метода зависит от точности приближения производных с помощью конечных разностей.

Если разности строятся по значениям функции f в произвольных узлах {xk}, то используются разделённые разности

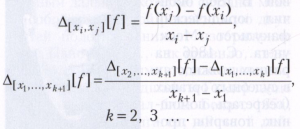
Справедлива общая формула

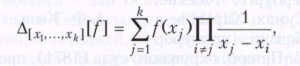
из которой следует, что значение разделённой разности не зависит от порядка аргументов х₁, ..., x_k. В терминах разделённых разностей просто записывается формула Ньютона для интерполяционного многочлена Pn(х), т. е. для многочлена, который совпадает с функцией f(x) в точках х₁, ..., x_n:

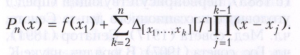
Одним из разделов конечных разностей исчисления является теория уравнений в конечных разностях, в которой изучаются, в частности, методы решения уравнений вида

F(x,f(x),Δ¹_h[f](x), ... , Δⁿ_h[f](x)) = 0,

где F - заданная, а f- искомая функция. Эта теория во многом аналогична теории дифференциальных уравнений. Наиболее разработаны случаи, когда функция F линейна по всем аргументам или по всем аргументам, кроме первого.

Лит.: Гельфонд А. О. Исчисление конечных разностей. 4-е изд. М., 2006; Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. 6-е изд. М., 2008.