Конус

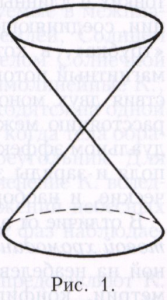КОНУС (коническая поверхность), множество прямых (образующих) евклидова пространства, проходящих через все точки некоторой линии (направляющей) и данную точку О пространства (вершину конуса). Если направляющая - прямая, то конус превращается в плоскость. Если направляющая - кривая 2-го порядка, не лежащая в одной плоскости с вершиной, то получается конус 2-го порядка (рис. 1, где направляющей служит эллипс). Простейшим из конусов 2-го порядка является прямой круговой конус, направляющей которого служит окружность, а вершина ортогонально проецируется в её центр. В этом случае конической поверхностью является совокупность всех прямых (образующих), проходящих через одну и ту же точку О и составляющих один и тот же угол с прямой, проходящей через центр окружности и точку О (осью конуса). Коническая поверхность имеет две полости, расположенные симметрично относительно вершины.

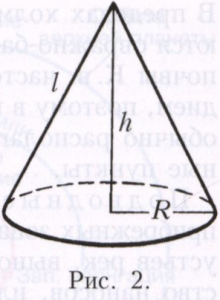Иногда конусом называют множество К, состоящее из всех полупрямых, исходящих из точки О и лежащих в одной из полостей конической поверхности. Часто конусом называют пересечение К с полупространством, содержащим О и ограниченным плоскостью, не проходящей через О (рис. 2). В этом случае часть плоскости, лежащая внутри конической поверхности, называется основанием конуса, а часть конической поверхности, заключённой между вершиной и основанием, - боковой поверхностью конуса.

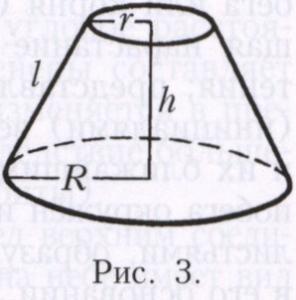Если основание прямого кругового конуса есть круг радиуса R, а длина отрезка между вершиной и основанием (высота конуса) равна h, то объём такого конуса равен πR²h/3; площадь боковой поверхности равна nRl, где l - длина отрезка образующей между вершиной и основанием. Часть конуса, заключённая между двумя параллельными плоскостями, называется усечённым конусом, или коническим слоем (рис. 3). Слой прямого кругового конуса между плоскостями, параллельными основанию, имеет объём π(R² + r² + Rr)h/3, где R и r - радиусы оснований усечённого конуса, h - его высота, т. е. отрезок, соединяющий центры его оснований, площадь боковой поверхности πl(R + r), где l - длина отрезка образующей.