Корреляции коэффициент

КОРРЕЛЯЦИИ КОЭФФИЦИЕНТ, числовая характеристика совместного распределения двух случайных величин, характеризующая их взаимосвязь. Корреляции коэффициент ρ = ρ (Х, Y) для случайных величин Х и Y с математическими ожиданиями а_X = ЕХ и а_Y = ΕY и ненулевыми дисперсиями σ²_X = DX и σ²_Y = DY определяется равенством

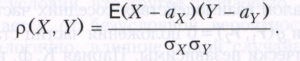
Корреляции коэффициент  для X и Y совпадает с ковариацией для величин (Χ - а_X)/σ_X и (Y - а_Y)/σ_Y, называемых нормированными. Корреляции коэффициент  симметричен относительно Х и Y и инвариантен относительно изменения начала отсчёта и масштаба, т. е. ρ (Х, Y) = ρ (Y, Х), и для любых чисел b₁, b₂ > 0, -∞ < с₁, с₂ < ∞ справедливо равенство ρ (b₁Х + с₁, b₂Y + с₂) = ρ (Х, Y). Абсолютная величина корреляции коэффициента не превосходит единицы. Корреляции коэффициент обладает следующими свойствами, характеризующими взаимосвязь случайных величин Х и Y:

если величины Х и Y независимы, то ρ (Х, Y) = 0 (обратное утверждение в общем случае неверно), о величинах, для которых ρ (Х, Y) = 0, говорят, что они некоррелированы;

|ρ (Х, Y)| = 1 тогда и только тогда, когда величины Х и Y связаны линейной функциональной зависимостью.

Трудность интерпретации корреляции коэффициента как меры взаимосвязи заключается в том, что равенство ρ (Х, Y) = 0 может иметь место и для зависимых случайных величин, в общем случае для независимости Х и Y необходимо и достаточно равенство нулю их максимального корреляции коэффициента, который определяется как точная верхняя грань (по функциям φ и ψ) корреляции коэффициента между случайными величинами φ(X) и ψ(Y). Однако вычисление максимального корреляции коэффициента представляет собой сложную задачу. Т.о., корреляции коэффициент не исчерпывает все виды зависимости между случайными величинами, он является лишь мерой их линейной связи. Эта линейная связь характеризуется следующим образом: величина

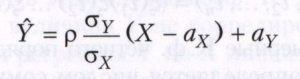
даёт линейное приближение Y с помощью Х, наилучшее в том смысле, что

(смотри также Регрессионный анализ).

А. В. Прохоров.