Корреляция в математике

КОРРЕЛЯЦИЯ в математике, зависимость между случайными величинами, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной зависимости корреляция, как правило, рассматривается тогда, когда одна из величин зависит не только от данной другой величины, но и от ряда иных случайных факторов. Зависимость между двумя случайными событиями проявляется в том, что условная вероятность одного из них при условии, что другое произошло, отличается от безусловной вероятности. Аналогично, влияние одной случайной величины на другую характеризуется условными распределениями одной из них при фиксированных значениях другой.

Пусть Х и Y - случайные величины с заданным совместным распределением вероятностей, а_X и а_Y - математические ожидания, σ²_X и σ²_Y - дисперсии и ρ-корреляции коэффициента случайных величин Х и Y. Если для каждого возможного значения х случайной величины Х определено условное математическое ожидание y(x)=Е(Y|Х=х), то функция у(х) называется регрессией величины Y по Х. Для оценки того, насколько точно регрессия передаёт изменение Y при изменении Х, используется условная дисперсия Y при данном значении X = х или её средняя величина (мера рассеяния Y около линии регрессии), равная

σ²_Y|X = Е(Y - Е(Y|Х))².

Если Х и Y независимы, то условные математические ожидания Y не зависят от х и совпадают с безусловным, т. е. у(х) = a_Υ, при этом σ²_Y|X = σ²_Y. При функциональной связи между Y и Х величина Y при каждом данном Х = х принимает одно значение и σ²_Y|X =0. Аналогично определяется х(у) = Е(Х|Y = у) - регрессия Х по Y. Показателем концентрации распределения вблизи линии регрессии у(х) служит корреляционное отношение

Величина η²|_Χ равна нулю тогда и только тогда, когда регрессия имеет вид у(х)=a_Y, в этом случае коэффициент корреляции р равен нулю и величина Y не коррелирована с Х. Если регрессия Y по Х линейна, т. е. линия регрессии - прямая, имеющая вид

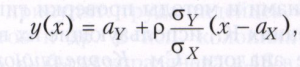
то σ²_Y|X = σ²_Y(1-ρ²) и η²_Y|X = ρ². Если, кроме того, |ρ| = 1, то Y связана с Х точной линейной зависимостью, если же η²_Y|X = ρ² < 1, то между Y и Х нет точной функциональной зависимости. Точная функциональная зависимость Y от Х, отличная от линейной, имеет место тогда и только тогда, когда ρ² < η²_Y|X = 1. Практическое использование коэффициента корреляции в качестве меры отсутствия зависимости оправданно (за редким исключением) лишь тогда, когда совместное распределение Х и Y нормально (или близко к нормальному распределению), так как в этом случае из равенства ρ = 0 следует независимость Х и Y. Для произвольных случайных величин Х и Y использование р как меры зависимости часто приводит к ошибочным выводам, так как р может равняться нулю даже при функциональной связи между величинами. Если совместное распределение Х и Y нормально, то обе линии регрессии у(х) и х(у) суть прямые, при |ρ| = 1 прямые регрессии сливаются в одну, что соответствует линейной зависимости между Х и Y, при ρ = 0 величины Х и Y независимы.

При изучении связи между несколькими случайными величинами Х₁,...,Х_n с заданным совместным распределением используется корреляционная матрица, элементами которой являются обычные коэффициенты корреляции ρ_ij между X_i и X_j, i, j= 1,..., n. Мерой линейной корреляции между Х₁ и совокупностью остальных величин Х₂,...,X_n служит множественный коэффициент корреляции, который определяется как обычный коэффициент корреляции между Х₁ и наилучшим линейным приближением Х₁ по Х₂,...,X_n, то есть между X₁ и β₁+β₂Χ₂+...+β_nХ_n, где числа β₁,...,β_n определяются так, чтобы дисперсия величины Х₁ - (β₁ + β₂Χ₂ + ··· + β_nХ_n) была минимальной. Множественный коэффициент корреляции выражается через элементы корреляционной матрицы, например при n = 3 он равен

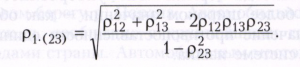
Если предполагается, что изменение величин Х₁ и Х₂ определяется в какой-то мере изменением остальных величин Х3 ,..., Хn, то показателем линейной связи между Х₁ и Х₂ при исключении влияния Х₃ ,..., Х_n является частный коэффициент корреляции между Х₁ и Х₂ относительно Х₃ ,..., Х_n, который определяется как обычный коэффициент корреляции между Х₁ - Х₁* и Х₂ - Х₂*, где Х₁*, Х₂* - соответственно наилучшие линейные приближения Х1 и Х₂ по Х₃ ,..., Х_n. Например, в случае n = 3 этот коэффициент равен

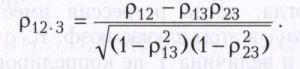
В математической статистике разработаны методы оценки корреляции между случайными величинами и методы проверки гипотез о значениях корреляции, использующие их выборочные аналоги. Смотри Корреляционный анализ.

Лит.: Кендалл М., Стьюарт А. Статистические выводы и связи. М., 1973.