Ковариация

КОВАРИАЦИЯ, числовая характеристика совместного распределения вероятностей двух случайных величин Х и Y с конечными дисперсиями DX и DY, она обозначается cov(Х, Y) и определяется равенством

где Е обозначает математическое ожидание. При этом

Для дисперсии суммы случайных величин Х и Y справедливо равенство

Если величины Х, Y независимы, то cov(Х, Y) = 0. Случайные величины Х, Y, для которых cov(Х, Y) = 0, называются некоррелированными. Из некоррелированности Х, Y, вообще говоря, не следует независимость Х и Y. Для нормально распределённых случайных величин Х и Y из некоррелированности следует их независимость. Попарная некоррелированность случайных величин Х₁, Х₂,..., является достаточным условием выполнения больших чисел закона в форме Чебышева: при любом ε > 0 и n → ∞

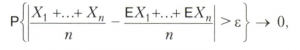
если дисперсии этих случайных величин ограничены одной и той же постоянной. С помощью ковариации определяется корреляции коэффициент.

В математической статистике оценкой ковариации служит выборочная ковариация, вычисляемая по формуле

где (X_i , Y_i), i = 1, 2,..., n, - независимые случайные величины, имеющие то же распределение, что (Х, Y) (выборка), а

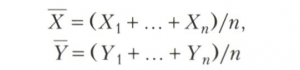
- выборочные средние. Величина

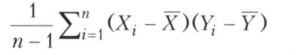
даёт несмещенную оценку ковариации.

С. Я. Шоргин.