Кратный интеграл

КРАТНЫЙ ИНТЕГРАЛ, интеграл от функции многих переменных f(х₁ ,..., x_m), m≥2, взятый по области m-мерного пространства. При m=2 кратный интеграл называют двойным интегралом, при m= 3 - тройным.

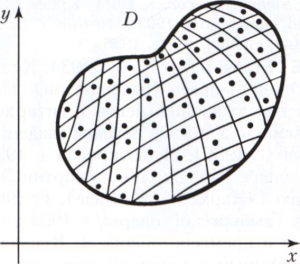
Характерным примером являются двойные интегралы. Пусть функция f(х, у) задана в квадрируемой области D на плоскости. Область D разбивают на n частичных областей d_i, которые имеют площади s_i. В каждой области d_i произвольным образом выбирается (смотри рисунок) точка (x_i,y_i) и составляется интегральная сумма

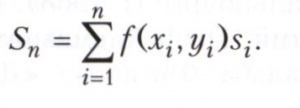
Если при неограниченном уменьшении максимального диаметра областей d_i, i = 1, ..., n, суммы S_n имеют предел, не зависящий от выбора областей d_i и точек (x_i, y_i), то этот предел называют двойным интегралом от функции f(х, у) по области D и обозначают

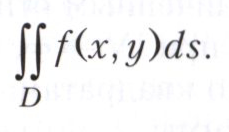
Если функция f непрерывна и область D замкнута, то интеграл заведомо существует. Аналогично определяются тройной интеграл и вообще m-кратные интегралы.

На кратный интеграл переносятся многие свойства интеграла Римана по отрезку (линейность, аддитивность относительно области интегрирования, возможность интегрирования неравенств и др.). Вместе с тем интегрируемая функция многих переменных может быть и неограниченной на D.

Для вычисления кратных интегралов их обычно сводят к интегралам от меньшего числа переменных (смотри Повторный интеграл). Для приближённого вычисления используют так называемые кубатурные формулы.

Кратные интегралы имеют различные применения, с их помощью выражаются объёмы и массы тел, статические моменты, моменты инерции и т. п.

Лит.: Никольский С. М. Курс математического анализа. М., 1991. Т. 2; Фихтенгольц Г. М. Основы математического анализа. 7-е изд. М., 2002. Т. 2; Ильин В. А., Садовничий В. А., Сендов Бл. Х. Математический анализ. 2-е изд. М., 2004. Ч. 2.