Кратный ряд

КРАТНЫЙ РЯД, формально записанная сумма

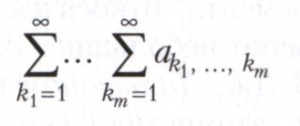
бесконечного набора слагаемых, зависящих от m индексов, m ≥ 2. Слагаемые a_{k1 ,..., km} называются членами ряда, они могут быть числами, функциями и другими объектами.

Характерные особенности кратного ряда по сравнению с обычными рядами (одномерными, при m = 1) видны на примере двойных числовых рядов, когда m= 2.

Как и для обычных рядов (смотри Ряд), сходимость двойного ряда понимается как сходимость его частичных сумм и суммой ряда называется предел частичных сумм, если он существует, при этом для двойных рядов нет единого определения частичных сумм. В разных случаях естественными оказываются различные определения частичных сумм. Наиболее часто рассматривают частичные суммы вида

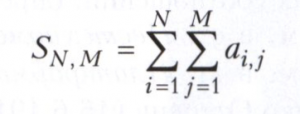
и двойной ряд называют сходящимся по прямоугольникам (или по Прингсхейму) к числу S, если суммы стремятся к S, когда N и М неограниченно возрастают независимо друг от друга. Если существуют положительные постоянные С₁ и С₂ такие, что S_N,М → S при N, М → ∞ так, что выполняются неравенства

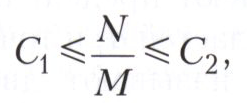
то говорят о сходимости по прямоугольникам с ограниченным отношением. Если S_N,_N→S при N→∞ то говорят о сходимости по квадратам. Если берутся частичные суммы

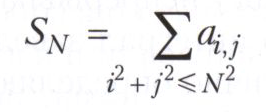
и S_N →S при N→∞, то говорят о сходимости по кругам.

Многие свойства кратных рядов существенно отличаются от свойств одномерных рядов. Например, члены сходящихся по Прингсхейму рядов не обязательно ограничены.

Для представления функций двух переменных f(х, у) используются двойные степенные ряды

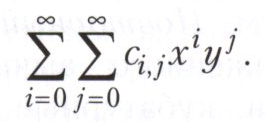
Лит.: Никольский С. М. Курс математического анализа. М., 1990. Т. 1; Воробьев Н. Н. Теория рядов. 6-е изд. СПб., 2002.