Квадратичное отклонение

КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ (квадратичное уклонение, стандартное уклонение, среднее квадратичное отклонение) величин х₁, . . . , х_n от заданной величины а  определяется равенством

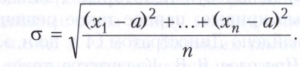
Наименьшее значение квадратичного отклонения достигается при а = xˉ, где  xˉ = (х₁ +  . . . + х_n)/n - среднее арифметическое величин х₁, . . . , х_n. В этом случае квадратичное отклонение может служить мерой рассеяния величин х₁, . . . , х_n. Иногда употребляют взвешенное квадратичное отклонение, равное

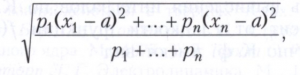
при этом положительные числа р₁, . . . , р_n называются весами, соответствующими величинам х₁, . . . , х_n. Взвешенное квадратичное отклонение достигает наименьшего значения при а, равном взвешенному среднему

В вероятностей теории квадратичное отклонение σ_Х случайной величины Х (от её математического ожидания) называется положительный квадратный корень из её дисперсии. В математической статистике квадратичное отклонение употребляют как меру качества статистических оценок и называют в этом случае квадратичной ошибкой.    

В. И. Битюцков.