Квадратурные формулы

КВАДРАТУРНЫЕ ФОРМУЛЫ, формулы приближённого вычисления определённого интеграла от функции f(х) по её значениям в конечном числе точек. Погрешность вычисления интегралов по квадратурным формулам зависит от гладкости функции f(х). Обычно квадратурные формулы имеют вид

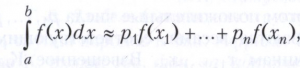
где х₁, . . . , х_n - точки отрезка [а,b], их называют узлами квадратурной формулы, а р₁, . . . ,р_n - числа, их называют коэффициентами (или весами) квадратурной формулы. Часто отрезок [а, b] разбивают на конечное число отрезков, на каждом из которых используют какую-либо простую квадратурную формулу. Простейшими квадратурными формулами являются формула прямоугольников

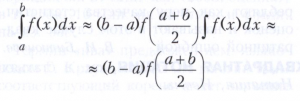
и формула трапеций

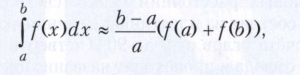
они дают точное значение интеграла для линейных функций. Формула Симпсона

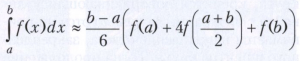
даёт точное значение интеграла для многочленов 3-й степени.

Для приближённого вычисления кратных интегралов используются аналогичные формулы, которые называют кубатурными.

Для вычисления, в первую очередь кратных интегралов, используют также формулы со случайным выбором узлов и коэффициентов (смотри Монте-Карло метод).

Лит.: Крылов В. И. Приближенное вычисление интегралов. 2-е изд. М., 1967; Крылов В. И., Шульгина Л. Т. Справочная книга по численному интегрированию. М., 1968.