Квадрупольный момент

КВАДРУПОЛЬНЫЙ МОМЕНТ, мультипольный момент 2-го порядка (ранга), характеризующий источники какого-либо поля. Квадрупольным моментом системы электрических зарядов, распределённых в объёме V с плотностью ρ(r), называется симметричный тензор

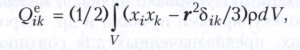
где x_i, x_k — компоненты радиус-вектора r, δ_ik- символ Кронекера, i, k = 1,2,3. Поскольку ∑³_i=1Q^e_ii = 0, то в общем случае имеется всего пять независимых составляющих электрического квадрупольного момента; из них собственно квадрупольным моментом иногда называют только диагональную составляющую Q^e₃₃. Если электрический дипольный момент р^е и суммарный электрический заряд q системы равны нулю, то тензор электрического квадрупольного момента не зависит от выбора начала отсчёта (точки r = 0). Потенциал электростатического поля стационарной системы зарядов на расстояниях R, больших по сравнению с её размерами l (R >> l), с учётом первых трёх мультипольных моментов имеет  вид  φ = q/R + p^en/R² + 3Q^e_ikn_in_k /R³ (по повторяющимся индексам i и k производится суммирование). Здесь используется система единиц Гаусса, вектор n = R/R задаёт направление от центра системы (r = 0) в точку наблюдения R. Квадрупольная составляющая потенциала соответствует полю сосредоточенного (точечного, l → 0) электрического квадруполя.

Аналогично для описания магнитостатического поля стационарной системы электрических токов с плотностью j(r) вводится симметричный псевдотензор магнитного квадрупольного момента

где × - знак векторного произведения, с - скорость света. В случае изменяющихся во времени систем электрических зарядов и токов тензоры электрического Q^e_ik и магнитного квадрупольных моментов характеризуют полное электромагнитное поле, создаваемое этими системами (смотри Квадрупольное излучение).

Лит.: Джексон Дж. Классическая электродинамика. М., 1965; Терлецкий Я. П., Рыбаков Ю. П. Электродинамика. 2-е изд. М., 1990; Ландау Л. Д., Лифшиц Е. М. Теория поля. 8-е изд. М., 2003.