Кватернионы

КВАТЕРНИОНЫ, обобщение понятия комплексных чисел. Комплексные числа х + iy, где х и у - действительные числа, i - базисная единица, удовлетворяющая условию i² = -1, изображаются геометрически точками (х, у) плоскости, и действия над ними соответствуют простейшим геометрическим преобразованиям плоскости (сдвигу, вращению, растяжению или сжатию и их комбинациям). Поиски числовой системы, которая геометрически реализовалась бы с помощью точек 3-мерного пространства, привели к установлению того, что из точек пространства трёх и выше измерений нельзя построить числовую систему, в которой алгебраические операции сохраняли бы все свойства сложения и умножения комплексных чисел. Из точек пространства четырёх измерений можно построить числовую систему, если отказаться от свойства коммутативности умножения, сохранив все остальные свойства сложения и умножения. Числа, составляющие такую систему, называются кватернионами; они представляют собой линейные комбинации

четырёх базисных единиц 1, i, j, k, где х₀, х₁, х₂, х₃ - действительные числа. Действия над кватернионами производятся по обычным правилам действия над многочленами относительно 1, i, j, k, (нельзя лишь использовать коммутативность умножения), правила умножения базисных единиц состоят в следующем:

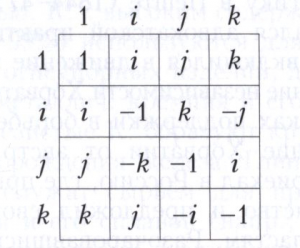
Базисная единица 1 играет роль обычной единицы и в записи кватерниона опускается, т. е. Х записывают в виде Х = х₀ + х₁i + + х₂ j  + х₃k. В Х различают скалярную часть х₀ и векторную часть V = х₁i + + х₂ j  + х₃k, так что Х = х₀ +V. Если х₀ = 0, то Х = V называется вектором; его можно отождествить с обычным 3-мерным вектором. Произведение кватернионов Х₁ = V₁ и Х₂ = V₂ выражается через скалярное (V₁,V₂) и векторное [V₁,V₂] произведения векторов V₁ и V₂ следующим образом:

что показывает тесную связь кватернионов с векторным исчислением.

Всякому кватерниону Х = х₀ + V можно сопоставить сопряжённый кватернион  Х = х₀-V, при этом

Это неотрицательное число называется нормой кватерниона Х и обозначается N(Х); она удовлетворяет соотношению N(XY) = N(Х)N(Y). У каждого кватерниона Х есть единственный обратный кватернион  Хˉ¹ (т.е. такой, что  ХХˉ¹ = Хˉ¹Х =1),  он  равен   X/N(X). Это даёт возможность решать уравне­ния вида ХА = В и AY = B: Х = ВАˉ¹ Y =Аˉ¹В; таким образом, кватернионы образуют алгебру с делением.

Обобщением комплексных чисел и кватернионов являются гиперкомплексные числа ранга n, которые представляют собой линейные комбинации х₀ + x₁e₁ + ... + x_n-1e_n-1 некоторой системы базисных единиц 1,e₁,...,e_n-1 с действительными коэффициентами  х₀ , x₁, ...,  x_n-1. Сложение и вычитание гиперкомплексных чисел определяется, как и в любом векторном пространстве, покомпонентно. Чтобы задать в этой системе умножение, надо определить (n - 1)² значений для произведений базисных единиц е_iе_j, i,j=1,...,n-1 (произведения на единицу определяются естественным образом: 1∙e_i = e_i∙1 =e_i, то есть задать матрицу порядка n - 1 так называемых структурных констант). Из гиперкомплексных чисел кватернионы оказываются в некотором смысле самыми близкими к действительным и комплексным числам. Точнее, все конечномерные действительные ассоциативные алгебры без делителей нуля исчерпываются полями действительных чисел R, комплексных чисел С и телом кватернионов.

Кватернионы  были введены У. Гамильтоном в 1843 году. В середине 19 века кватернионы воспринимались как обобщение понятия числа, призванного играть в науке столь же значительную роль, как и комплексные числа. Эта точка зрения подкреплялась тем, что были найдены приложения кватернионов к электродинамике и механике. Однако векторное исчисление в его современной форме вытеснило кватернионы из этих областей. Роль кватернионов несравнима с ролью комплексных чисел, имеющих многочисленные и разнообразные приложения в различных отраслях науки и техники.

Лит.: Кантор И. Л., Солодовников А. С. Гиперкомплексные числа. М., 1973; Калужнин Л. А. Введение в общую алгебру. М., 1973.