Ван дер Ваальса уравнение

ВАН ДЕР ВААЛЬСА УРАВНЕНИЕ, уравнение состояния реального газа. Предложено Й. Д. Ван дер Ваальсом в 1873 году. Для газа, содержащего N молекул, Ван дер Ваальса уравнение имеет вид:

где V - объём, ρ - давление, Т - абсолютная температура газа, k - постоянная Больцмана, а и b - характерные для данного вещества постоянные, учитывающие притяжение и отталкивание молекул. Член aN²/V² называется внутренним давлением, постоянная b равна учетверённому объёму молекулы газа, если в качестве модели молекул принять слабо притягивающиеся упругие сферы. Ван дер Ваальса уравнение количественно определяет свойства реальных газов лишь в области относительно высоких температур Т и низких давлений ρ, так как а и b являются функциями температуры. С дальнейшим ростом Т и понижением ρ оно переходит в уравнение состояния идеального газа (Клапейрона уравнение). Однако Ван дер Ваальса уравнение качественно правильно описывает поведение газа и жидкости и при высоких ρ, а также особенности фазового перехода между ними. Ван дер Ваальса уравнение описывает, кроме того, критическое и метастабильное состояния системы жидкость – газ.

Изотерма, описывающая критическое состояние вещества, имеет в некоторой (критической) точке как максимум, так и точку перегиба, то есть (дρ/дV)Т = 0, (д²ρ/дV²)Т = 0. Решение системы из этих двух уравнений и Ван дер Ваальса уравнения даёт возможность установить связь между параметрами критического состояния и константами Ван дер Ваальса уравнения:

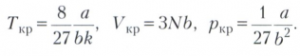
Введя безразмерные приведённые переменные Т_ПР=Т/Т_КР, ρ_ПР=ρ/ρ_ΚР, V_ПP  = V/V_KP, можно получить приведённое уравнение состояния:

оно имеет более широкое применение, чем Ван дер Ваальса уравнение, поскольку не зависит явно от параметров а и b.

Лит.: Кубо Р. Термодинамика. М., 1970.