Жидкость

ЖИДКОСТЬ, агрегатное состояние вещества, занимающее промежуточное положение между газообразным и твёрдым кристаллическими состояниями. Область существования жидкости ограничена со стороны низких температур фазовым переходом в твёрдое состояние (кристаллизацией), а со стороны высоких температур - в газообразное (испарением). По химическому составу различают однокомпонентные, или чистые, жидкости и двух- или многокомпонентные жидкие смеси (растворы). Химически чистые однокомпонентные жидкости могут быть разделены на нормальные (простые) и ассоциированные. К первым относятся одноатомные жидкости, такие как сжиженные благородные газы, жидкие металлы, а также ряд многоатомных жидкостей. Ко вторым относится значительное число многоатомных органических жидкостей, на свойства которых в заметной степени оказывают влияние слабые химические взаимодействия (водородные связи). Особое место занимают жидкие кристаллы с сильно выраженной анизотропией и квантовые жидкости, обладающие специфическими квантовыми свойствами при очень низких температурах.

Свойства жидкостей. По ряду свойств жидкости близки к твёрдым (кристаллическим) телам: сохраняют объём, образуют поверхность, обладают определённой прочностью на разрыв. В то же время между твёрдым телом и жидкостями имеются существенные различия. Жидкость  отличает от твёрдых тел большая подвижность отдельных молекул, поэтому в ней при приложении малых сдвиговых напряжений не возникает упругой деформации, а появляется сила вязкого сопротивления. Коэффициент динамической вязкости жидкости вблизи точки плавления в 10¹³ раз меньше, чем у твёрдого тела, а коэффициент самодиффузии в 10⁵ раз больше. Вместе с тем жидкости обладают свойствами, сближающими их с газами: принимают форму сосуда, в который помещены; в области состояний, называемой закритической, они непрерывно переходят в газообразное состояние, не испытывая скачка плотности. Однако есть и существенные различия в свойствах жидкости и газов. Например, плотность жидкости примерно в тысячу раз больше плотности газов. Кроме того, в поведении некоторых свойств жидкостей и газов наблюдаются качественные различия. Так, вязкость газов увеличивается с ростом температуры, а вязкость жидкостей, напротив, уменьшается. В отличие от газов для жидкостей характерно возрастание с температурой отношения c_p/c_V, в газах c_p/c_V = const (с_р - теплоёмкость при постоянном давлении, c_V - теплоёмкость при постоянном объёме).

Значения коэффициентов переноса газов и жидкостей сильно различаются. Так, например, для жидкого кислорода при температуре 100 К коэффициент вязкости η = 0,16·10^-3 Па·с, коэффициент теплопроводности λ = 135·10^-3 Вт/м·К. В газовой фазе при температуре 300 К и атмосферном давлении те же величины имеют значения 0,027·10^-3 Па·с и 26,7·10^-3 Вт/м·К соответственно.

Основой для количественного описания термодинамических свойств жидкости является уравнение состояния. Ван дер Ваальса уравнение, не являясь универсальным в строгом смысле, качественно правильно описывает поведение жидкости и газа в широком диапазоне давлений р и температур Т, а также особенности фазового перехода между ними.

Присутствие в жидкости сильного межмолекулярного взаимодействия обусловливает наличие у неё поверхностного натяжения на границе её с любой другой средой. Благодаря поверхностному натяжению жидкость стремится принять такую форму, которая обеспечивает минимальную площадь её поверхности при заданном объёме. При отсутствии внешних сил, когда действуют только межмолекулярные силы (например, в условиях невесомости), жидкость приобретает форму шара. Влияние поверхностного натяжения на движение границ жидкости с твёрдыми телами или границ между несмешивающимися жидкостями относится к области капиллярных явлений.

Механические свойства жидкостей описываются набором законов сохранения (числа частиц, импульса и энергии). Движения жидкостей, рассматриваемых как сплошные среды, изучаются в гидродинамике.

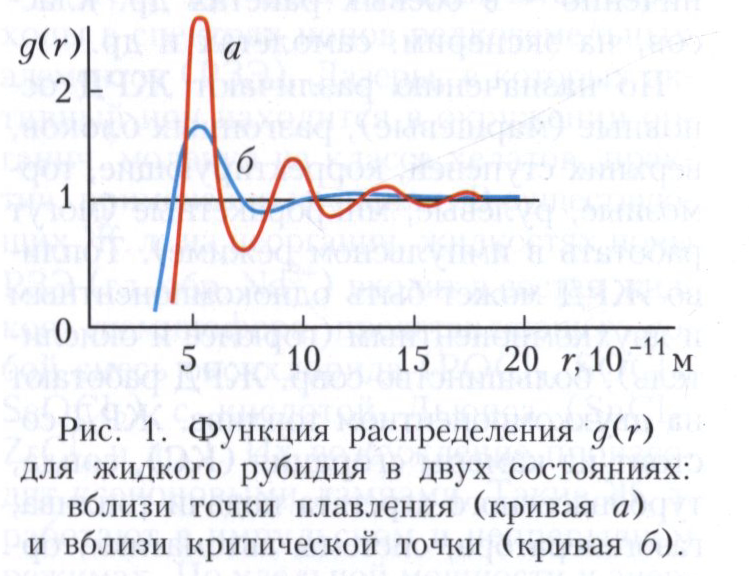
Структура жидкостей. Согласно данным рентгено- и нейтронографии, структура жидкости обладает ближним порядком и в ней отсутствует дальний порядок (смотри Дальний и ближний порядок). Это значит, что в положении ближайших соседей любой молекулы наблюдаются лишь незначительные отклонения от правильной псевдокристаллической упаковки. Однако небольшие отклонения от правильной упаковки быстро накапливаются, и уже на расстоянии нескольких периодов невозможно обнаружить такую же молекулу с окружением, отвечающим ожидаемому порядку. Количественной структурной характеристикой жидкости является радиальная функция распределения g(r), определяющая вероятность, с которой на расстоянии r от выбранной молекулы может быть встречена другая молекула. Функцию g (r) находят из экспериментальных данных по рассеянию рентгеновских лучей или медленных нейтронов (из углового распределения интенсивности рассеянных лучей). Непосредственно из опыта может быть получена так называемая функция рассеяния (структурный фактор) S(Q), которая представляет собой фурье-образ функции g(r). На рисунке 1 изображена функция g(r) для жидкого рубидия. Наличие нескольких максимумов у радиальной функции распределения свидетельствует о локальном упорядочении молекул на расстояниях порядка нескольких молекулярных диаметров. С увеличением температуры, т. е. по мере уменьшения плотности жидкости, максимумы радиальной функции распределения проявляются менее отчётливо, что указывает на уменьшение степени молекулярного упорядочения. С помощью радиальной функции распределения может быть определено среднее число N ближайших соседей выбранной молекулы. В отличие от твёрдых тел в жидкостях тепловое расширение сопровождается существенным изменением именно этого параметра: например, в криптоне при изменении плотности от значения, соответствующего точке плавления, до значения, соответствующего критической точке, N уменьшается от 8,5 до 4. При этом среднее межатомное расстояние увеличивается всего лишь на 5%, в то время как удельный объём возрастает в 2,5 раза.

Одной из центральных проблем в исследовании простых жидкостей является определение связи между радиальной функцией распределения g(r) и парным потенциалом межмолекулярного взаимодействия ф(r). Известно несколько приближений, позволяющих рассчитывать структурные характеристики жидкости по заданным парным потенциалам. Одно из приближений (интегральное уравнение Перкуса - Йевика) позволило выразить в аналитической форме связь g (r) с простым парным потенциалом, отвечающим модели жёстких (непритягивающихся) сфер. Этот результат сыграл большую роль в развитии методов термодинамической теории возмущений, в которой в качестве нулевого приближения используется радиальная функция распределения модели жёстких сфер. Многочисленные исследования, проведённые методом рассеяния рентгеновских лучей и нейтронов, показали, что структура простых жидкостей вблизи точки плавления хорошо моделируется структурой, формируемой молекулами в виде твёрдых сфер при соответствующих плотностях.

Молекулярно-кинетическая теория жидкостей. Различие в свойствах жидкости, твёрдых тел и газов тесным образом связано с различиями в микроскопической структуре и в характере молекулярного теплового движения. В жидкости тепловое движение молекул носит локально коллективный характер в отличие от их беспорядочного движения в газах и коллективного движения в твёрдых телах. В жидкости тепловое движение молекул происходит следующим образом. Молекула совершает нерегулярные колебания со средней частотой 1/τ₀, близкой к максимальной частоте колебаний частиц в кристалле, и амплитудой, определяемой так называемым свободным объёмом, не занятым соседями. На основе модельных представлений о свободном объёме получают наиболее простые выражения для коэффициентов переноса.

Свободный объём не является постоянной величиной, а распределяется между частицами в самых разных долях. Центр колебаний молекулы в жидкости перемещается вследствие подвижности окружающих молекул. Перемещение молекулы из одного положения равновесия в другое происходит скачком с преодолением потенциального барьера W (энергия активации). Среднее время τ пребывания молекулы в одном равновесном положении, или «время оседлой жизни» молекул в жидкости, пропорционально τ₀ехр(W/kT), где k - постоянная Больцмана, Т - температура. Коэффициент диффузии D обратно пропорционален τ, поэтому

В этих модельных представлениях вязкость η как величина, обратная текучести, описывается экспонентой с положительным показателем, то есть

[где А(Т) - функция, слабо зависящая от температуры], и, следовательно, должна уменьшаться с ростом температуры. Последнее выражение, известное как формула Андраде, довольно точно описывает коэффициент сдвиговой вязкости как простых, так и сложных многоатомных жидкостей при постоянном давлении. Увеличение текучести, сопровождающее рост температуры жидкости, в значительной мере обусловлено увеличением свободного объёма, что явным образом учитывает формула Бачинского - полуэмпирическое соотношение, согласно которому зависимость коэффициента вязкости η от температуры Т и давления р описывается с помощью одной переменной - удельного объёма v:

где В и b - постоянные, причём h приблизительно равна постоянной b в уравнении Ван дер Ваальса, знаменатель v-b представляет собой свободный объём жидкости Из этой формулы следует, что в условиях постоянства давления вязкость не зависит от температуры. В действительности в условиях компенсации теплового расширения путём увеличения давления вязкость жидкости при повышении температуры уменьшается, хотя и существенно медленнее, чем в условиях постоянства давления. Удельный объём является определяющим параметром и в описании теплопроводности жидкости. Например, коэффициент теплопроводности органической жидкости в температурной области до точки нормального кипения хорошо описывается формулой Предводителева: λ = Βν^-4/3, где В - константа.

Определение свойств жидкости возможно не только на основе простых физических моделей. Успешное развитие методов компьютерного моделирования молекулярных процессов (например, метод Монте-Карло) позволило получить более точные представления о явлениях переноса на молекулярном уровне. Так, новые данные о коэффициенте переноса были получены из анализа автокорреляционной функции скорости, которая определяется следующим образом:

где V(t) и V(t + τ) - два значения скорости одной и той же молекулы в разные моменты времени, разделённые интервалом τ. Угловые скобки означают усреднение по времени, V̅² - среднее значение произведения скоростей при τ = 0, ψ(τ) - безразмерная функция времени. Рассмотрение диффузии как процесса случайного блуждания частиц приводит к следующему соотношению между коэффициентами самодиффузии D и автокорреляционной функцией:

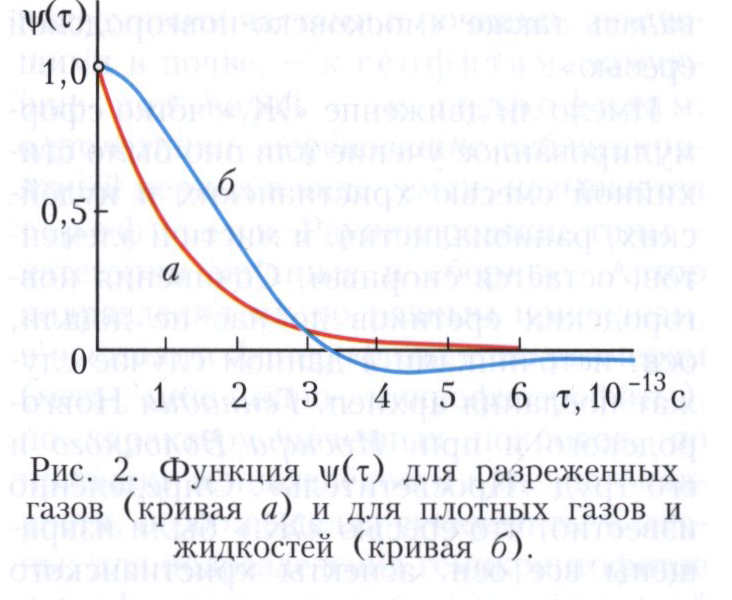
Для разреженного газа функция ψ(τ) пропорциональна exp(-kT/Dm) (кривая а на рисунке 2), где m - масса частицы. Метод молекулярной динамики позволяет определить вид ψ(τ) для модельной среды с заданным парным потенциалом, плотностью числа частиц и температурой. Для плотных газов и жидкостей ψ(τ) имеет вид знакопеременной функции (кривая б на рисунке 2), что связано с высокой вероятностью изменения знака скорости частицы через время τ > τ_и [τ_и - момент пересечения функцией ψ(τ) оси времени; величина порядка 10^-13 с]. Отрицательная область объясняется «рассеянием назад» частицы внутри свободного объёма, создаваемого ближайшими соседями.

Строгая молекулярно-кинетическая теория явлений переноса в жидкостях строится на основе данных о неравновесных функциях распределения, которые находятся из решения интегро-дифференциальных уравнений. Эти уравнения содержат член, описывающий обмен импульсами при столкновениях. Его вид зависит от выбранной модели молекулярного теплового движения. Модель Райса - Олнетта основана на том, что частица, участвующая в молекулярном тепловом движении, испытывает два вида воздействий со стороны своего окружения. Во-первых, она находится в молекулярном поле, создаваемом ближайшими соседями. Под действием этого флуктуирующего поля молекула испытывает слабые, но частые толчки. Изменение импульса молекулы описывается кинетическим уравнением диффузионного типа (Фоккера - Планка уравнение), которое можно интерпретировать как уравнение, отображающее броуновское движение в импульсном пространстве. Во-вторых, импульс молекулы может сильно изменяться в результате парного соударения с молекулой, имеющей значительную скорость. Такого рода столкновения описываются кинетическим уравнением Больцмана. Поскольку между этими актами столкновения импульс молекулы многократно изменяется, то последствия предыдущего сильного толчка «забываются» и при очередном сильном столкновении можно пренебречь корреляцией скоростей сталкивающихся молекул. Теория Райса - Олнетта представляет собой комбинацию уравнения Фоккера - Планка и уравнения Больцмана, усовершенствованного С. Чепменом и шведским учёным Д. Энскогом. Теория позволила рассчитать абсолютные значения коэффициентов вязкости и теплопроводности аргона при минимальной исходной информации.

Методы молекулярной динамики позволяют моделировать тепловое движение большого числа частиц при заданном законе их взаимодействия. Анализ индивидуальных и коллективных движений молекул даёт возможность проверки различных теорий жидкого состояния.

Лит.: Гиршфельдер Дж., Кертисс Ч., Берд Р. Молекулярная теория газов и жидкостей. М., 1961; Фишер И.З. Статистическая теория жидкостей. М., 1961; Физика простых жидкостей / Под редакцией Г. Темперли и др. М., 1971. Ч. 1-2; Френкель Я. И. Кинетическая теория жидкостей. Л., 1975; Крокстон К. Физика жидкого состояния. М., 1978.