Волновое уравнение

ВОЛНОВОЕ УРАВНЕНИЕ, линейное однородное дифференциальное уравнение в частных производных, описывающее распространение волн в среде; имеет вид:

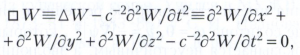
где t - время, х, у, z -пространственные декартовы координаты, W = W(х, у, z, t) - функция, характеризующая возмущение среды в точке с координатами х, у, z в момент времени t, с - параметр с размерностью скорости, ? - оператор Д’Аламбера (даламбертиан), Δ - оператор Лапласа (лапласиан). Первоначально волновое уравнение было получено для одномерного случая практически одновременно (40-е годы 18 века) Д. Бернулли, Ж. Д’Аламбером и Л. Эйлером.

Одномерное волновое уравнение совпадает с уравнением колебаний идеально упругой струны:

решение которого может быть представлено в виде двух волн, перемещающихся в пространстве со скоростью с:

Каждая из этих волн и составляет моду, распространяющуюся только в одном направлении (+х или -х) и удовлетворяющую волновому уравнению 1-го порядка (уравнению волны):

Волновое  уравнение допускает разделение переменных по координатам и времени: W = W₁(х, у, z)φ(t). При гармонической зависимости от времени, выраженной с помощью комплексной записи φ = ехр(iωt), где ω = kс, k - волновое число, волновое уравнение превращается в уравнение Гельмгольца:

которое в двумерном случае даёт уравнение мембраны, а в одномерном - уравнение осциллятора.

Волновое  уравнение может быть неоднородным, если в его правой части стоит заданная функция координат и времени, т. е.

Неоднородное волновое уравнение кроме собственных решений - нормальных волн, существующих независимо от внешнего источника, - имеет и вынужденное решение, описывающее колебания, волны и другие движения, возбуждённые источником.

Волновое  уравнение описывает почти все разновидности малых колебаний в распределённых механических системах: продольные звуковые колебания в газе, жидкости, твёрдом теле, поперечные колебания в струнах, на поверхности жидкости и др. Волновым  уравнениям  удовлетворяют компоненты векторов электромагнитного поля и потенциалов, поэтому многие электромагнитные явления (в диапазоне частот от квазистатических до оптических) описываются с их помощью. В нелинейных средах такие явления, как взаимодействие монохроматических волн, возникновение и эволюция ударных волн и солитонов, самофокусировка и самоканализация волн, могут быть описаны с помощью нелинейных волновых уравнений. В квантовой механике иногда Шрёдингера уравнение называют волновым уравнением.

Лит.: Уизем Дж. Линейные и нелинейные волны. М., 1977.