Волны

ВОЛНЫ, изменения во времени (возмущения) каких-либо физических параметров среды (полей), распространяющиеся в пространстве и переносящие энергию и информацию. Волновые процессы различной природы играют исключительно важную роль в природе и жизни человека. Так, поступающая от Солнца на Землю энергия переносится в основном электромагнитными волнами различного диапазона. Благодаря световому и радиоизлучению мы получаем информацию об удалённых космических объектах, в том числе находящихся «на краю Вселенной». Волновой характер имеют электрические импульсы, распространяющиеся по нервным волокнам живых организмов (смотри Нервный импульс). Микрообъекты, изучаемые в квантовой физике, обладают свойствами не только частиц, но и волн (смотри Корпускулярно-волновой дуализм, Волны де Бройля).

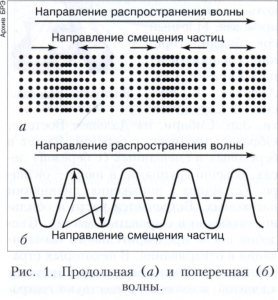Наиболее привычными с древнейших времён являются волны на поверхности жидкости, для которых характерно перемещение колебаний её уровня, хотя сама жидкость в целом может оставаться неподвижной. В объёмах жидкостей и газов могут распространяться продольные упругие волны сжатия и разрежения (акустические волны, в том числе звуковые), в которых смещения частиц среды происходят вдоль направления распространения волны (рис. 1а). В твёрдых средах могут существовать также и поперечные волны, в которых смещения происходят поперёк направления распространения волны (рис. 1б). Такие волны обоих типов, пронизывающие всю толщу Земли, возникают при землетрясениях. Поперечными являются и изгибные волны в струнах и стержнях. Необходимое условие распространения волновых движений с конечной скоростью - наличие инерции среды и локальной (близкодействующей) связи между изменениями параметров в соседних её точках, приводящей к появлению возвратной силы. Так, в случае продольной волны сжатие среды в некоторой области приводит к повышению давления в ней и передаче движения в соседние области. Упругие волны и волны на поверхности жидкости фактически являются распространяющимся возмущением среды (отклонением от состояния равновесия), однако электромагнитные волны (свет, радиоволны и др.), представляющие собой взаимосвязанные пространственно-временные изменения электрических и магнитных полей, поперечных к направлению распространения, существуют и в вакууме. Общая теория относительности предсказывает также возможность распространения в вакууме гравитационных волн.

Во всех случаях, когда перенос волновых возмущений от одной точки пространства к другой происходит в результате причинно-следственных связей между полями в этих точках, скорость их распространения не может превышать скорость света с в вакууме. Однако при использовании источников, специально расположенных вдоль некоторой линии, можно создавать возмущения, перемещающиеся вдоль неё со сколь угодно большой (в том числе сверхсветовой) скоростью. В чисто кинематическом смысле такие процессы иногда тоже называют волнами, но при этом не происходит переноса энергии и в динамическом смысле подобный процесс волной не является.

Бегущие волны, фазовая и групповая скорости. Простейшим и типичным примером волновых движений являются бегущие волны, в которых соответствующая динамическая переменная s (например, давление в звуковой волне) зависит от времени t и одной пространственной координаты Х по закону:

s(х, t) = F(х-vt),

где F - произвольная функция. Величина s остаётся постоянной при х-vt =  const, и весь профиль волны перемещается вдоль оси Х без искажений со скоростью v = Δх/Δt; такие волны называются стационарными. Значение v зависит от конкретной волновой системы; так, для электромагнитных волн в изотропной непроводящей среде v = ε/(εμ)^1/2, где ε и μ - диэлектрическая и магнитная проницаемости среды, а в жидкостях и газах скорость звука определяется их адиабатической сжимаемостью. Выражение s(х,t) является решением волнового уравнения

d²s/dx² - v^-2d²s/dt² = 0,

называемого в одномерном случае уравнением Д’Аламбера.

Пространственно-временная структура реальных волновых полей может быть разнообразной - в виде отдельных импульсов, цугов (ограниченного ряда повторяющихся возмущений) и достаточно близкой к периодической. Особо важное значение имеют и находят широкое применение волны, близкие к синусоидальным (называемым гармоническими), когда характеризующая волновое поле динамическая величина описывается выражением:

s(x, t) =А sin φ(х, t), φ(x, t) = ωt - kx + φ₀,

где А - амплитуда (наибольшее смещение от положения равновесия), φ₀ - начальная фаза волны, ω = 2π/Т- угловая частота колебаний, k = 2π/λ - волновое число, λ - длина волны (расстояние между соседними максимумами или минимумами), Т - период (время, за которое совершается полный цикл колебаний). Точки с постоянной фазой φ(х, t) = const (волновой фронт) при этом перемещаются в пространстве с фазовой скоростью vф = ω/k = λ/Т. Имея в виду подобные «бегущие» колебательные структуры, волну иногда определяют как распространяющиеся колебания. Во многих волновых системах значение v различно на разных частотах (имеет место дисперсия волн), зависимость v(ω) или эквивалентное ей соотношение ω(k) называется дисперсионным уравнением. Для электромагнитных волн дисперсия определяется частотной зависимостью параметров ε и μ среды; в вакууме ε = μ = 1 и дисперсии нет (скорость волны не зависит от их частоты и равна с). Для волн в плазме, однако, эта дисперсия весьма существенна. В большинстве жидкостей дисперсия акустической волны достаточно мала. Длинные поверхностные волны на «мелкой воде» (глубина слоя жидкости <λ) распространяются быстрее коротких. Это справедливо и для возникающих при землетрясениях мощных волнах - цунами.

В общем случае фазу плоской волны можно записать в виде: φ(r, t) = ωt - kr, где k - волновой вектор, перпендикулярный фронту волны, r - радиус-вектор точки пространства.

Используемые на практике волны (сигналы) не являются строго гармоническими: либо амплитуда, либо фаза, либо частота их плавно изменяются в масштабах Т и λ (модулируются; смотри Модуляция колебаний и волн), причём переносимая сигналом информация кодируется именно законом модуляции. В диспергирующей среде различие фазовых скоростей отдельных спектральных составляющих приводит к тому, что огибающая сигнала в общем случае распространяется с так называемой групповой скоростью, отличной от фазовой скорости на несущей частоте ω: ω_гр = dω/dk = v - λdv/dλ.

Именно групповая скорость волны представляет собой реальную скорость распространения сигнала, в том числе переноса энергии, и релятивистское ограничение относится именно к ней (v_гp<с); фазовая же скорость волны в принципе может превышать скорость света. Возможны и такие волновые системы, когда фазовая и групповая скорости направлены в противоположные стороны, такие волны называются обратными волнами.

В линейных диспергирующих системах форма огибающей волны остаётся неизменной только на ограниченных расстояниях. На больших расстояниях начинаются искажения; в частности, короткие импульсы начинают расплываться, так как разные спектральные составляющие сигнала распространяются с различной скоростью. На таких расстояниях понятие групповой скорости уже теряет физический смысл.

Интерференция волн. Волны  любой природы способны интерферировать. Под интерференцией понимается взаимное усиление или ослабление двух или большего числа волн, перекрывающихся в пространстве, в зависимости от соотношения их фаз. Суммарная интенсивность двух гармонических волн с одинаковыми частотами и амплитудами A₁ и А₂ в области их перекрывания равна

А² = А₁² +A²₂ + 2A₁A₂cos Δφ;

разность полных фаз волн Δφ различна в разных точках пространства. В тех точках, где Δφ = 0 (или кратно целому числу 2π), результирующая амплитуда равна сумме амплитуд (А=А₁+А₂), а в точках с противоположными фазами |A| = |A₂-А₁|, при A₁=A₂ в этих точках одна волна полностью «гасит» другую. В результате в пространстве образуются поверхности минимумов и максимумов интенсивности колебаний (рис. 2), структура которых зависит от формы фазовых фронтов интерферирующих волн.

Фактически это означает перераспределение энергии волнового поля в пространстве. В частности, для двух плоских волн с одинаковыми амплитудами и нулевыми начальными фазами, распространяющихся навстречу друг другу вдоль оси х, суммарное поле имеет вид стоячей волны;

s(x, t) = 2A₁coskxcosωt.

В точках х = 0 или mλ/2 (m - целое число) расположены «пучности» стоячей волны, в них амплитуда максимальна и равна 2А, на расстоянии λ/4 от них находятся «узлы», где амплитуда равна нулю. Для упругих волны узлам волн давления соответствуют пучности колебательной скорости, и наоборот; узлы и пучности электрического и магнитного полей электромагнитной волны также сдвинуты на λ/4. Поэтому в стоячей волне в среднем не происходит направленного переноса энергии.

Для наблюдения интерференционных картин существенное значение имеет когерентность волн. Фазы реальных источников и излучаемых ими волн неизбежно испытывают случайные флуктуации, и если вызванные ими уходы разности фаз Δφ сравнимы или превышают π/2, то положения максимумов и минимумов также хаотическим образом будут перемещаться в пространстве. Тогда при инерционном наблюдении интерференционная картина будет размываться. В акустических и радиодиапазонах обычно этот фактор мало существен, однако в оптическом диапазоне ситуация другая. При использовании естественных источников света время, в течение которого фазу волны можно считать постоянной, при нормальных условиях составляет всего 10^-9-10^-10 с. Кроме того, фаза волны испытывает также случайные флуктуации в плоскости фронта волны. Поэтому интерференцию света долго не удавалось наблюдать экспериментально, и лишь в начале 19 века проблему удалось впервые решить, используя метод разделения источников (смотри Интерференция света). С появлением источников когерентного света - лазеров - создание и наблюдение интерференции света не представляет сложности.

Неоднородные среды, преломление и отражение волн. Плоские бегущие волны, строго говоря, могут существовать только в однородном пространстве. Когда имеется резкая (в масштабе длины волны λ) граница раздела двух сред, возникает отражение волн и преломление волн (их проникновение во вторую среду) (рис. 3). Если падающая волна и сама граница плоские, то плоскими будут прошедшая и отражённая волна. Связь параметров этих волн определяется граничными условиями, вытекающими из уравнений динамики соответствующего волнового поля. В частности, для электромагнитных волн - это условия непрерывности тангенциальных компонент векторов напряжённости электрического и магнитного полей, в случае упругих волн - условия непрерывности давления и колебательного смещения частиц среды по обе стороны от границы. В изотропных средах угол отражения α_отр равен углу падения α₀, а угол преломления α_пр удовлетворяет закону Снелла: v₂sinα₀ = v₁sinα_np. Для электромагнитных волн в непроводящей и немагнитной среде коэффициенты отражения и преломления определяются Френеля формулами. Эти коэффициенты оказываются различными для разных поляризаций падающей волны Если вектор напряжённости электрического поля падающей волны лежит в плоскости падения, то при угле падения α₀ таком, что выполняется условие tgα₀ = n₂/n₁ (n₁, n₂ - показатели преломления сред), отражённая волна не возникает (смотри Брюстера закон), тогда как для другой поляризации (электрическое поле перпендикулярно плоскости падения) отражение есть всегда. В результате при отражении меняется характер поляризации волны. В анизотропных средах прошедшие волны разных поляризаций имеют разные углы преломления (смотри Двойное лучепреломление). Сильное влияние на отражательную способность материалов оказывает их электрическая проводимость; в частности, большинство металлов являются хорошими отражателями в оптическм и радиодиапазонах.

Последовательные отражения волн в направлении их распространения от двух или большего числа поверхностей могут привести к их волноводному распространению. Волноводы широко применяются в радио- и оптическом диапазонах, а также в акустике. Используя несколько хорошо отражающих поверхностей, можно создавать резонаторы, волновое поле которых замкнуто в ограниченном объёме. Простейший пример такого резонатора для электромагнитных волн (часто применяемый в оптическом диапазоне, в том числе в лазерах) - интерферометр Фабри - Перо, представляющий собой систему из двух параллельных зеркал, между которыми устанавливается стоячая волна. При идеально проводящих зеркалах на их поверхностях оказываются узлы электрического поля, поэтому внутри такого резонатора могут существовать лишь волны с дискретными значениями волнового числа.

Если же среда является плавно неоднородной, то волновое поле можно считать «квазиплоским» - на расстояниях порядка λ изменения амплитуды А и волнового вектора k будут достаточно малыми. В таких случаях широко используется приближение геометрической оптики, в основе которой лежит представление волнового поля в виде набора независимых лучей. В изотропной среде направление луча совпадает с волновым вектором k, плавное преломление луча в неоднородной среде называется рефракцией. Термин «геометрическая оптика» обычно используют не только для световой волны, но и для волны любой физической природы (в акустике аналогичное приближение называется геометрической акустикой). Рефракция волны в среде с плавным изменением показателя преломления в поперечном направлении также может привести к волноводному распространению.

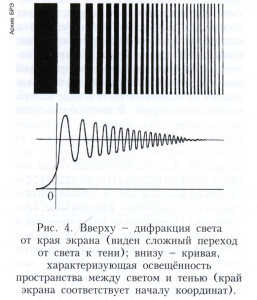Волновые пучки. Дифракция волн. При нормальном падении плоской волны на непрозрачный экран с отверстием d за экраном, согласно законам геометрической оптики, должен распространяться параллельный пучок шириной d с резкой границей света и тени. Однако независимо от физической природы волны такой вывод оказывается справедливым только до расстояний от экрана порядка r < d²/λ (эта область называется ближней зоной). На больших расстояниях пучок начинает искажаться - волновое поле «затекает» в зону геометрической тени, а в «освещённой» области появляются максимумы и минимумы интенсивности. Эти явления, заключающиеся в отклонении реальных волновых полей от предсказываемых законами геометрической оптики, называются дифракцией волн. При обратном неравенстве r >> d²/λ (дифракция Фраунгофера) волновой фронт становится локально сферическим с угловой шириной пучка α = λ/d. Причина дифракционных искажений пучка заключается в том, что, в отличие от идеальной плоской волны, ограниченный по ширине пучок содержит в своём пространственном спектре пакет волновых векторов с угловым разбросом порядка λ/d. Для приближённого расчёта дифракционных задач удобен и широко применяется Гюйгенса - Френеля принцип, согласно которому волновое поле в произвольной точке вне источника может быть найдено в виде суперпозиции волны (с учётом их интерференции) от вторичных источников, располагаемых на замкнутой поверхности, окружающей первичный источник; если на пути между первичной (освещающей) волной и точкой наблюдения имеется непрозрачный экран, амплитуда вторичных источников в соответствующих местах принимается равной нулю. На рисунке 4 приведена картина, наблюдаемая при дифракции света от края непрозрачного экрана. Острые максимумы, образующиеся при дифракции Фраунгофера, можно формировать, используя дифракционные решётки - периодические структуры из щелей или отражателей; такие решётки используются в качестве спектральных приборов. В более широком смысле к дифракционным относятся все эффекты, возникающие при распространении волны в средах, содержащих любые неоднородности, в том числе малые по сравнению с λ.

Дифракция ограничивает предельные возможности различных устройств, использующих волновое излучение, причём естественным масштабом, определяющим эти пределы, является длина волны. Так, слаборасходящийся волновой пучок возможен лишь, если его ширина намного превышает λ. Различные фокусирующие устройства (линзы, зеркала и их комбинации) не могут сфокусировать излучение в область размером, меньшим λ. Разрешающая способность приборов, строящих изображение, в том числе оптических микроскопов, также ограничивается длиной волны, поэтому для получения изображений более мелких структур, размерами меньшими λ, используется электронный микроскоп.

Излучение волн. Эффект Доплера. Источниками волн могут служить любые внешние воздействия, выводящие волновую систему (среду, поле) из состояния равновесия; при этом возбуждаемые волны уносят с собой энергию, расходуемую источником. Колеблющееся в упругой среде тело излучает акустические волны, источником электромагнитных волн являются переменные токи, т. е. ускоренно движущиеся заряды, например электрический диполь с периодически изменяющимся во времени дипольным моментом. В общем случае энергия излучения распределяется по различным направлениям неравномерно.

Излучение волны возможно и при равномерном движении тел, движущихся в какой-либо среде со скоростью, превышающей скорость распространения волны в этой среде. Так, движущийся со сверхзвуковой скоростью (v>v_3В) самолёт или снаряд возбуждает ударные волны, распространяющиеся под углом θ = arccos(v_ф/v) к направлению движения тела (Маха конус). В среде без дисперсии этот конус одинаков для всех частот, в результате на фронте такой волны образуется резкий скачок давления - ударная волна. Такую же природу имеет «носовая волна» на поверхности воды, возникающая при движении судов. Электрический заряд, движущийся в диэлектрической среде со сверхсветовой скоростью v>с/n, излучает электромагнитные волны (Вавилова - Черенкова излучение). Излучение возможно и при v<с/n, если среда неоднородна; например, когда заряд пересекает границу двух сред (так называемое переходное излучение).

Если источник волн и их приёмник (наблюдатель) неподвижны, то в линейной среде частота принимаемых волны совпадает с частотой источника. Если же источник движется, то частота волн, принимаемых неподвижным наблюдателем, зависит от направления движения источника. При движении источника к неподвижному наблюдателю (или наблюдателя к неподвижному источнику) принимаемая частота ω будет больше, чем частота ω₀ при неподвижном источнике; при удалении источника от наблюдателя частота принимаемого наблюдателем излучения будет меньше. Такое изменение частоты при взаимном движении источника и приёмника волны называется Доплера эффектом; этот эффект кинематический и имеет место для волны любой физической природы.

Изменение частоты волн возможно также в процессе их распространения в нестационарной среде, параметры которой меняются во времени. Так, при отражении волны от движущейся навстречу границы частота отражённой волны повышается.

Нелинейные волны. При достаточно больших амплитудах волн начинают проявляться различные нелинейные эффекты (смотри Нелинейная оптика, Нелинейная акустика). Так, для поверхностных волн на мелкой воде скорость движения гребней оказывается больше, чем скорость впадин, поэтому по мере их распространения происходит укручение переднего фронта, приводящее в конечном счёте к их обрушению. Подобная нелинейная трансформация акустической волны приводит к образованию ударной волны, а первоначально синусоидальный профиль на некотором расстоянии становится пилообразным (рис. 5).

Подобная трансформация профиля волн, возможная и в других волновых системах без дисперсии, в том числе электромагнитных, означает появление в её спектре большого числа высших гармоник. При наличии заметной дисперсии образование скачкообразных фронтов уже невозможно, и нелинейная эволюция волн имеет более сложный характер, зависящий от соотношения параметров нелинейности и дисперсии. При определённых условиях могут существовать стационарные бегущие волны, профиль которых при малых амплитудах близок к синусоиде, а при больших - к последовательности коротких импульсов. В пределе бесконечного периода получаются уединённые волны - солитоны, они имеют тем меньшую длительность и большую скорость распространения, чем выше их амплитуда.

Нелинейность может существенно влиять на распространение волновых пучков. Если, например, показатель преломления среды n зависит от интенсивности волны I так, что dn/dI > 0, то пучок со спадающей к краям интенсивностью сам создаёт условия, способствующие его волноводному распространению, что может уменьшить или даже скомпенсировать дифракционную расходимость, в результате происходит самофокусировка пучка (смотри Самофокусировка света). По этой причине, в частности, мощные лазерные пучки обычно оказываются неустойчивыми и распадаются на отдельные «нити».

Если в пространстве перекрываются две интенсивные волны (в том числе и различной физической природы), происходит их нелинейное взаимодействие (смотри Взаимодействие волн), в частности, низкочастотная волна может модулировать высокочастотную. Если частоты исходных волн равны соответственно ω₁ и ω₂, в спектре появляются комбинационные частоты lω₁ + mω₂, где l и m - целые числа. Так, при одновременном выполнении двух равенств: ω₃ = ω₁ ± ω₂ и k₃ = k₁ ± k₂ (называемых условиями фазового синхронизма) происходит эффективная генерация суммарной или разностной частоты. При тех же условиях возможен и обратный процесс - «распад» волны с частотой ω₃ на две с частотами ω₁, ω₂; подобные резонансные взаимодействия могут происходить и с участием четырёх и большего числа волн (смотри, например, Взаимодействие световых волн). Существенное значение нелинейные процессы имеют в активных средах, в которых возникающие волновые возмущения не поглощаются, а, наоборот, усиливаются (в частности в лазерах). Именно нелинейные факторы, наряду с дисперсией, определяют амплитуду, форму и спектр генерируемых такими системами колебаний. При некоторых условиях эти колебания могут стать нерегулярными (хаотическими, смотри Динамический хаос, Автоволны).

Лит.: Горелик Г. С. Колебания и волны. 2-е изд. М., 1959; Виноградова М. Б., Руденко О. В., Сухорукое А. П. Теория волн. 2-е изд. М., 1990; Рыскин Н.М., Трубецков Д. И. Нелинейные волны. М., 2000; Трубецков Д. И., Рожнев А. Г. Линейные колебания и волны. М., 2001.