Возмущений теория

ВОЗМУЩЕНИЙ ТЕОРИЯ, общее название комплекса методов исследования различных задач. Возмущений теория применяется в тех случаях, когда при исследовании физического (в широком смысле) процесса (например, движения планет Солнечной системы) установлены математические соотношения (например, дифференциальные уравнения), которым удовлетворяют характеристики изучаемого процесса (например, координаты планет), причём эти соотношения содержат малый параметр ε (или несколько таких параметров), и при ε = 0 система этих соотношений допускает достаточно простое решение. Истинное поведение изучаемого процесса рассматривается как «возмущение» процесса, соответствующего значению ε = 0. Задача возмущений теории состоит в том, чтобы, отправляясь от известных результатов для ε = 0, найти поправки к ним, которые позволяют с достаточной точностью определить значения изучаемых величин и при ненулевых, хотя и малых, значениях ε.

Например, для планет Солнечной системы параметры ε характеризуют малость взаимного притяжения планет по сравнению с их притяжением Солнцем. При ε = 0 учитывается только притяжение планет Солнцем, так что их движение описывается Кеплера законами. С привлечением возмущений теории более точное описание движения планет может быть получено с учётом влияния взаимного притяжения всех или наиболее крупных планет.

Общая схема применения возмущений теории по-разному конкретизируется в различных задачах. В самом широком плане основная часть возмущений теории распадается на возмущений теории для дифференциальных уравнений (например, упомянутая задача о планетах) и на возмущений теории для операторов в функциональном анализе (например, ряд задач квантовой механики). Вне этих рамок (хотя и в идейной связи с основной частью возмущений теории) находятся применения своеобразных вариантов возмущений теории в статистической физике и квантовой теории поля. Имеются также пограничные области, отнесение которых к возмущений теории зависит от конкретного содержания, вкладываемого в это понятие.

Во многих случаях вычисляемые величины могут быть представлены в виде ряда по степеням ε, что может быть сделано сравнительно несложно. Однако такой прямой подход даже в простых задачах может быть неадекватным в том смысле, что полученный результат может не отражать специфики явления. Пусть, например, изучается колебание, характеризуемое некоторой величиной х, периодически изменяющейся со временем t по закону х = sin ωt, причём зависимость частоты ω от ε выражается степенным рядом ω = ω₀ + ω₁ε + ω₂ε² + .... При прямом подходе получается, что

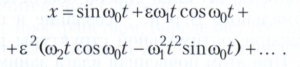
Эта формула не отражает периодичности функции х(t) и даже может создаться впечатление, будто с ростом t величина х(t) может стать очень большой. Поэтому при применении возмущений теории приходится использовать другие (не прямые) подходы, при которых тем или иным способом учитывается возможность изменения частоты колебаний, но сохраняется колебательный характер процесса и при ε ≠ 0. Это говорит о том, что в ряде случаев возмущений теория смыкается с другими разделами теории дифференциальных уравнений или теории операторов.

В более сложных случаях ряд по степеням ε может расходиться, часто его можно понимать как асимптотическое разложение, что иногда достаточно для целей исследования.

Сказанное выше относится к основной части возмущений теории. Иногда приходится выходить за пределы основной части возмущений теории. Так, с привлечением КАМ-теории в некоторых задачах возмущений теории можно получать более точные результаты. В случаях, когда поправки при использовании возмущений теории имеют высокий порядок малости, также нужен выход за пределы основного ядра возмущений теории. КАМ-теория и нахождение экспоненциальных поправок - примеры упоминавшихся выше пограничных с возмущений теорией областей.

Лит.: Крылов Н. М., Боголюбов Н. Н. Введение в нелинейную механику. К., 1937; Биркгоф Дж. Д. Динамические системы. М.; Л., 1941 ; Боголюбов Н. Н. О некоторых статистических методах в математической физике. К., 1945; Маслов В. П. Теория возмущений и асимптотические методы. М., 1965; Шарлье К. Небесная механика. М., 1966; Боголюбов Н. Н., Логунов А.А., Тодоров И. Т. Основы аксиоматического подхода в квантовой теории поля. М., 1969; Като Т. Теория возмущений линейных операторов. М., 1972; Боголюбов Н. Н., Митропольский Ю. А. Асимптотические методы в теории нелинейных колебаний. 4-е изд. М., 1974; Моисеев Н. Н. Асимптотические методы нелинейной механики. 2-е изд. М., 1981; Блохинцев Д.И. Основы квантовой механики. 6-е изд. М., 1983; Боголюбов Н. Н., Ширков Д. В. Введение в теорию квантованных полей. 4-е изд. М., 1984 Арнольд В. И. Математические методы классической механики. 3-е изд. М., 1989.