Автоколебания

АВТОКОЛЕБАНИЯ, поддерживающиеся за счёт внешнего источника энергии колебания в физических, биологических и других системах, параметры которых (амплитуда, частота, спектр колебаний) определяются свойствами самой системы и не зависят от конечного изменения начальных условий. Системы, в которых возникают автоколебания, называются автоколебательными. Автоколебания могут быть периодическими, то есть точно воспроизводящими себя через период Т=1/f, где f - частота автоколебаний, или хаотическими, то есть нерегулярными (случайными). Спектр частот таких автоколебаний сплошной, а их статистические свойства не меняются во времени (смотри Хаос).

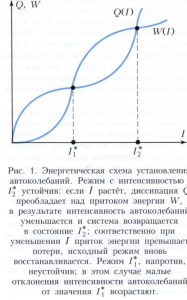Автоколебания возникают в системе произвольной природы в результате развития колебательных неустойчивостей с их последующей стабилизацией из-за прекращения поступления энергии от источника или прогрессирующего возрастания потерь энергии (диссипации). Для установившихся автоколебаний характерен средний по времени баланс потерь и подкачки энергии: потери энергии Q(I) (I - интенсивность автоколебаний) должны компенсироваться поступлением энергии W(I) от источника, то есть Q(I*) = W(I*). Если в окрестности стационарного режима I* энергия потерь при увеличении интенсивности автоколебаний растёт быстрее, чем приток энергии, то этот режим с энергетической точки зрения устойчив; если же быстрее увеличивается W(I), то стационарный режим неустойчив (рисунок 1). Уже из такого усреднённого описания видно, что установление автоколебания возможно лишь в диссипативных нелинейных системах.

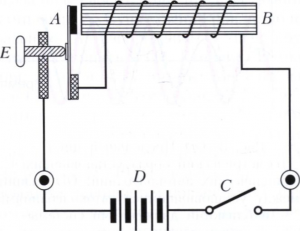
Термин «автоколебания» введён А. А. Андроновым в 1928 году. Достаточно полная теория автоколебания построена в 20 веке в работах Андронова, А. Пуанкаре, голландского учёного Б. Ван дер Поля и других. Изобретённый в 19 веке электрический прерыватель (звонок) - простейший пример автоколебательной системы (рисунок 2): при включении батареи в цепь питания катушки железный сердечник становится магнитом и притягивает молоточек. Цепь питания размыкается, сердечник перестаёт быть магнитом, и пружинка возвращает молоточек в исходное состояние. Цепь питания вновь замыкается, и процесс циклически повторяется. Как и во многих других системах с автоколебаниями, неустойчивость равновесного состояния здесь связана с наличием обратной связи - зависящее от силы притяжения сердечника положение молоточка управляет цепью питания сердечника. Частоту ударов молоточка можно регулировать, изменяя, например, жёсткость пружинки.

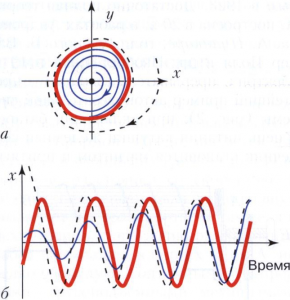
Поведение автоколебательной системы удобно представить в пространстве состояний (фазовом пространстве), координаты которого - переменные системы, например, ток в катушке электрического прерывателя и угол отклонения молоточка. Состоянию системы в данный момент времени отвечает точка в фазовом пространстве. Эволюции системы соответствует движение такой точки по траектории, называемой фазовой. Геометрическим образом установившихся автоколебаний в фазовом пространстве служит аттрактор - траектория (или множество траекторий), расположенная в ограниченной области фазового пространства и притягивающая к себе все близкие траектории. В системе с одним (глобальным) аттрактором свойства установившихся автоколебаний не зависят от начальных условий - со временем система их забывает. Это происходит тем быстрее, чем сильнее диссипация энергии в системе. Аттрактор, отвечающий периодическим автоколебаниям, - это предельный цикл - притягивающая замкнутая траектория (рисунок 3). Образом хаотических автоколебаний является странный аттрактор - притягивающее множество из неустойчивых траекторий.

Для многих химических, биологических и экономических систем характерны концентрационные автоколебания - колебания численности биологических популяций, объёмов производства и прочее. Такие автоколебания описываются кинетическими уравнениями, в которых учитывается рост и стабилизация численности внутри одного вида, а также взаимодействие между видами, питающимися из общего источника. Типичный механизм зарождения концентрационных автоколебаний - конкуренция. При этом «победа» для каждого из участников может оказаться лишь временной, и в результате последовательной смены «победителей» устанавливаются автоколебания. В химической реакции такая смена «победителей» может сопровождаться пульсациями окраски жидкой реакционной смеси. Например, при взаимодействии малоновой кислоты с броматом калия и другими реагентами в присутствии ферроина (реакция Белоусова - Жаботинского) цвет раствора циклически меняется во времени от голубого до красного. Если число конкурирующих видов достаточно велико, концентрационные автоколебания могут быть как регулярными, так и хаотическими.

Хаотические автоколебания наблюдаются, например, при термоконвекции вязкой жидкости, заключённой в вертикально расположенную кольцевую трубу. При подогреве снизу тёплая жидкость поднимается вверх, вытесняя более холодную жидкость вниз. Жидкость начинает вращаться. Если подогрев увеличить, скорость вращения возрастает, поднявшаяся наверх жидкость не успевает остыть и вращение на какой-то момент прекращается; после остановки, в силу симметрии системы, жидкость может начать вращаться и по часовой стрелке, и против. Подобные переключения направления вращения нерегулярны (режим периодических пульсаций скорости неустойчив). Рассмотренные автоколебания описываются моделью Лоренца (1963 год). В подобных системах хаос появляется не в результате действия внешних шумов или внутренних флуктуаций, а определяется собственно динамикой нелинейной системы, выражающейся в неустойчивости индивидуальных движений. Это в буквальном смысле - генератор хаоса - рождение случайного в неслучайной системе. Предсказать движения такой системы во времени возможно лишь в среднем.

Автоколебания наблюдаются и в протяжённых системах - неравновесных средах. Они могут иметь вид спиралей или двумерных вихрей, как в реакторе, где происходит автокаталитическая реакция Белоусова - Жаботинского, или локализованных состояний, как в процессах горения. Автоколебания с выраженной пространственной структурой называются автоволнами или автоструктурами, что подчёркивает независимость их свойств от условий на границах среды. Хаотические автоколебания в неравновесных средах - это турбулентность.

При наличии связи автоколебательных систем может наблюдаться явление синхронизации - взаимная подстройка ритмов пульсаций, генерируемых взаимодействующими системами (смотри Синхронизация колебаний и волн). Современные нейрофизиологические эксперименты показали, что синхронизация потенциалов действия, генерируемых нейронами, наблюдается в коре головного мозга и других отделах нервной системы животных и человека.

Теория автоколебания включает в себя построение базовых моделей, позволяющих описать механизмы рождения и установления автоколебания и определить их свойства в зависимости от параметров модели, исследовать взаимные трансформации различных режимов автоколебания - бифуркации, возникающие при изменении параметров, и, таким образом, предсказать все основные движения автоколебательной системы. Модели автоколебаний - это диссипативные динамические системы. Они определяются уравнениями (дифференциальными, разностными, в частных производных и так далее), допускающими существование на бесконечном интервале времени единственного решения для каждого начального условия. Состояние динамической модели описывается набором переменных, выбираемых из соображений естественности интерпретации измеряемых величин, простоты описания, симметрии и тому подобное. Обычно выделяют модели с непрерывным временем (потоки) и модели с дискретным временем (каскады или отображения). Дискретность времени часто не просто удобна для построения модели, но и отражает сущность процесса - дискретность моментов прохождения импульсов через активную среду в оптическом квантовом генераторе, смена поколений в генетике и другое. Вне границ бифуркаций динамической модели автоколебания являются грубыми (структурно устойчивыми): при малом изменении параметров модели её движения качественно не изменяются. Именно поэтому число базовых моделей автоколебания конечно.

Лит.: Ланда П. С. Автоколебания в системах с конечным числом степеней свободы. М., 1980; Андронов А. А., Витт А. А., Хайкин С.Э. Теория колебаний. 2-е изд. М., 1981; Рабинович М.И., Езерский А. Б. Динамическая теория формообразования. М., 1998; Рабинович М. И., Трубецков Д. И. Введение в теорию колебаний и волн. 3-е изд. М.; Ижевск, 2000.