Игр теория

ИГР ТЕОРИЯ, раздел математики, изучающий математические модели принятия решений в конфликтных ситуациях. Под конфликтной ситуацией, или просто конфликтом, понимается ситуация, в которой участвуют различные стороны (называемые игроками), имеющие несовпадающие интересы. Многие явления экономического, социального, правового, военного характера содержат конфликтные ситуации различной сложности, поэтому их математические модели, изучаемые в игр теории, весьма разнообразны.

Классы игр, основные понятия и результаты. Описание конфликтной ситуации в виде игры состоит в указании, кто и как участвует в конфликте, каковы возможные исходы конфликта, а также в какой степени участвующие в конфликте стороны заинтересованы в его исходах. Каждая игра характеризуется множеством игроков I = {1, ..., N}, семейством множеств {X_i}_iЄI, называемых стратегиями, и семейством функций выигрыша игроков {X_i}_iЄI, заданных на прямом произведении Х = Х₁^х... ^x X_N и принимающих действительные значения. Игра состоит в выборе каждым из игроков i Є I своей стратегии x_i Є X_i, в результате игры игрок i Є I получает выигрыш H_i(х₁, ..., x_N). Предполагается, что, выбирая стратегию, каждый из игроков стремится получить максимально возможный выигрыш. Предполагается также, что выбор стратегии каждым из игроков неизвестен остальным игрокам, поэтому игр теорию можно рассматривать как теорию принятия решений в условиях неопределенности.

В простейшем случае, когда N = 2 и Н₁ = -Н₂, игра называется антагонистической игрой двух лиц; при этом, если множества стратегий Х₁ и Х₂ конечны, Х₁ = {1, ..., m}, Х₂ = {1, .., n}, то игра называется матричной игрой, поскольку функцию Н₁, называемую функцией выигрыша первого игрока, можно задать m х n матрицей

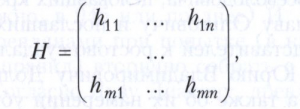
где h_ij = Н₁(i, j), i = 1, ..., m, j = 1, ..., n. Первый игрок может гарантировать себе выигрыш, равный

выбирая стратегию i₀, при которой функция min_jh_ij принимает максимальное значение. Аналогично, выбирая стратегию j₀, при которой max_ih_ij достигает минимума, второй игрок гарантирует, что его проигрыш не будет превышать

Для любой матричной игры v₁ ≤ ν₂.

Если v₁ = v₂, то пара (i₀, j₀) представляет собой седловую точку матрицы Н, то есть для неё выполняются неравенства h_ij0 ≤h_i0j0 ≤ h_i0j; при всех i= 1, ..., m,  j = 1, ...,n. В этом случае число называется значением (иногда ценой) игры, стратегии i₀ и j₀ называются оптимальными чистыми стратегиями соответственно первого и второго игроков, пара оптимальных стратегий называется решением игры. Оптимальные чистые стратегии существуют не для всех матричных игр. Если таких стратегий нет, то возможности игроков расширяют и оптимальные стратегии ищут в классе так называемых смешанных стратегий, т. е. в множестве стратегий, являющихся распределениями вероятностей на множествах чистых стратегий; иначе говоря, стратегиями являются распределения р = (р₁, ..., р_m), P_i ≥ 0, i =1, ..., m, р₁ + ... +р_m= 1, для первого игрока и распределения q = (q₁, …, q_n), q_j ≥ 0, j=1,...,n, q₁ + ... + q_n= 1, для второго игрока. В качестве выигрыша первого игрока в этом расширении матричной игры рассматривается математическое ожидание выигрыша исходной игры при выборе игроками смешанных стратегий р и q.

Основная теорема теории матричных игр, известная как теорема Неймана о минимаксе, утверждает, что в любой матричной игре существуют оптимальные смешанные стратегии р* и q* такие, что

для любых р и q, т. е. пара (р*, q*) представляет собой седловую точку функции Н(р, q). Величина v = Н(р*,q*) называется значением (или ценой) игры (в смешанных стратегиях). Справедливы равенства

Последнее равенство составляет содержание теоремы о минимаксе, являющейся одной из основных теорем теории игр.

Смысл оптимальных смешанных стратегий состоит в следующем. Пусть игра повторяется t раз и пусть первый игрок выбирает оптимальную смешанную стратегию р* =(р*₁, ..., р*_m), то есть в каждой игре он выбирает чистую стратегию i с вероятностью р*_i, i= 1,..,m. Выигрыш первого игрока в каждой игре - случайная величина, математическое ожидание которой конечно. Среднее значение выигрыша v_t за t игр при росте t в силу больших чисел закона и теоремы о минимаксе в пределе будет не меньше цены игры, какую бы смешанную стратегию ни выбрал второй игрок. Это среднее значение будет стремиться к v по вероятности, если второй игрок выберет свою оптимальную смешанную стратегию q*.

Основные методы нахождения решения матричных игр опираются на использование методов линейного программирования.

Другим большим классом антагонистических игр являются антагонистические игры, называемые играми на единичном квадрате, в которых множества чистых стратегий первого и второго игроков представляют собой сегмент [0, 1]. К игре на единичном квадрате может быть сведена любая антагонистическая игра с множествами стратегий обоих игроков, имеющими мощность континуума. Эти игры задаются функцией выигрыша К(х, у), определённой на единичном квадрате. Смешанными стратегиями игроков являются функции распределения F(х) и G(у), х Є [0,1], у Є [0,1]. При достаточно широких условиях на функцию К(х, у) выигрыш первого игрока при условии, что первый и второй игроки применяют соответственно смешанные стратегии F и G, полагается равным

и справедлива теорема о минимаксе

т. е. существуют значение игры v и оптимальные смешанные стратегии обоих игроков. Существуют игры на единичном квадрате, для которых теорема о минимаксе несправедлива.

Класс игр, в которых игроки применяют свои стратегии однократно и независимо от выбора противника, включает в себя и игры, осуществляемые путём последовательного выполнения ходов участниками. В таких играх выбор стратегии игрока состоит в указании выбора поочерёдно выполняемых ходов на основании сведений, быть может неполных, о предыдущих ходах обоих игроков, т. е. на основании сведений о текущей позиции игры, в которой принимается решение. Такие игры называются позиционными. Если при принятии решения об очередном ходе игроку известны все предыдущие ходы обоих игроков, то такая игра называется игрой с полной информацией.

В качестве примера позиционной игры с полной информацией можно привести шахматы. Т. к. правила выбора хода в любой позиции игры известны, в принципе можно выписать все стратегии обоих игроков в игре и указать результат каждой партии, сведя, таким образом, эту игру к матричной форме. Теорема Цермело - Неймана утверждает, что все позиционные игры с полной информацией имеют решение в чистых стратегиях. Для шахмат это означает, что если приписать победе первого игрока выигрыш, равный 1, ничьей - выигрыш, равный 0, и поражению - выигрыш, равный -1, то такая игра имеет значение в чистых стратегиях, равное 1, 0 или -1, но истинная величина этого значения неизвестна.

Потребности нахождения оптимального управления в конфликтных ситуациях привели к развитию теории позиционных игр с непрерывным временем, называемых дифференциальными играми. В дифференциальной игре предполагается, что движение управляемой системы описывается уравнением

где t - время, х -фазовый вектор, f(t, х, и, v) - некоторая функция, u = u(t, х(t)) и v = v(t, х(t)) - управляющие стратегии первого и второго игроков. В момент времени t игроки располагают информацией о текущей позиции (t, х(t)). Выигрыш (плата) в дифференциальной игре задаётся некоторым функционалом с(х(t), u(t), v(t)), первый игрок стремится добиться минимально возможного, а второй - максимально возможного значения функционала. Специфика дифференциальных игр не позволяет ограничить класс допустимых стратегий u(t, х(t)), v(t, х(t)) гладкими функциями и использовать для нахождения траектории х(t) известные методы теории обыкновенных дифференциальных уравнений. При некоторых условиях на функции, входящие в определение дифференциальной игры, игра имеет значение и оптимальные стратегии. Во 2-й половине 20 века глубокие связи дифференциальных игр с теорией оптимального управления были установлены Л. С. Понтрягиным, подход к дифференциальным играм как к позиционным играм с непрерывным временем разрабатывался российским математиком Н. Н. Красовским. Для нахождения решений дифференциальных игр может быть использовано динамическое программирование.

В случае неантагонистических игр принцип оптимальности трансформируется в требование приемлемости ситуаций. Ситуация (набор стратегий) х = (х₁, ..., x_N) в неантагонистической игре называется приемлемой для коалиции (группы игроков) K ⊂ I или, иначе, К-оптимальной, если отклонение игроков из К от своих стратегий не улучшает ситуацию с точки зрения коалиции К. При этом неулучшение может пониматься по-разному: как неувеличение выигрыша для всех игроков, входящих в К; неувеличение суммарного выигрыша всех игроков из К, возможность увеличения выигрыша одних игроков из К лишь за счёт уменьшения выигрыша других игроков из К. Для коалиции К ситуация, обладающая последним из перечисленных свойств, называется оптимальной по Парето. Ситуация, приемлемая для каждой коалиции из некоторого набора коалиций К={К₁ ..., К_m}, называется К-устойчивой. Если К состоит из всех отдельных игроков множества I, то К-устойчивая ситуация называется равновесной по Нэшу. Эти понятия находят широкое применение при анализе математических моделей конфликтных ситуаций в экономике.

Исторический очерк. Отдельные соображения по поводу математического описания конфликтных ситуаций высказывались начиная с 17 века многими учёными. В конкретных играх смешанные стратегии появились в начале 18 века. Ряд по существу теоретико-игровых утверждений в эквивалентной форме был получен в различных разделах математики, например П. Л. Чебышевым в теории приближения функций. В 1911 Э. Цермело описал теоретико-игровой подход к шахматной игре. В 1921 Э. Борель ввёл понятие чистых и смешанных стратегий в матричных играх, однако в полном объёме теорему о минимаксе он не доказал. Эта теорема теории матричных игр была доказана Дж. фон Нейманом в 1928 году. Он опубликовал статью «К теории стратегических игр» (1928), содержащую основные идеи современной игр теории, однако до 1944 эти идеи не получили широкого распространения. Их детальной разработке посвящена книга Дж. фон Неймана и О. Моргенштерна «Теория игр и экономическое поведение». После выхода этой книги игр теория вошла в число разделов современной математики и стала развиваться как из потребностей её экономических, социальных, правовых, военных и других применений, так и в силу своих внутренних потребностей. В СССР игр теория развивалась в основном ленинградской школой теории игр, созданной российским математиком Н. Н. Воробьёвым.

Лит. : Линейные неравенства и смежные вопросы / Под редакцией Г. У. Куна, А. У. Таккера. М., 1959; Льюс Р. Д., Райфа Х. Игры и решения. М., 1961; Карлин С. Математические методы в теории игр, программировании и экономике. М., 1964; Красовский Н.Н., Субботин А. И. Позиционные дифференциальные игры. М., 1974; Петросян Л. А. Дифференциальные игры преследования. Л., 1977; Математическая теория оптимальных процессов. 4-е изд., М., 1983; Воробьев Н. Н. Основы теории игр: Бескоалиционные игры. М., 1984.

В. Ф. Колчин.