Десятичная дробь

ДЕСЯТИЧНАЯ ДРОБЬ, дробь, знаменатель которой есть целая степень числа 10. Десятичную  дробь пишут без знаменателя, отделяя запятой (иногда точкой) в числителе справа столько цифр, сколько нулей содержится в знаменателе; если величина дроби меньше единицы, то перед запятой ставится нуль. Например, 123/10 = 12,3; 123/1000 = 0,123. Для положительной десятичной дроби принята запись

где 0 ≤a_i, b_j< 10, i = 0, 1, ..., k, j= 1, 2, ..., n - целые числа, причём если k ≠ 0, то и a_k ≠ 0. Под записью (1) пони­мается число, равное

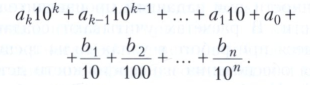
Цифры b₁,b₂......... b_n, стоящие после запя­той, называются десятичными знаками.

Бесконечной десятичной дробью называется запись вида

a, b₁b₂···,                           (2)

где а - целое число, а каждое из чисел b_j, j = 1, 2, ..., принимает одно из значе­ний 0, 1, 2, ..., 9. Любое положительное действительное число а является сум­мой ряда

Частные суммы ряда (2), конечные десятичные дроби а, b₁...b_n, являются приближёнными значениями числа α с недостатком, а числа

приближёнными значениями α с избытком. Если существуют такие числа n и m, что для всех i > n имеют место равенства b_i = b_i+m, то бесконечная десятичная дробь называется периодической, а число  m - периодом. Всякую конечную десятичную дробь можно рассматривать как бесконечную периодических дробь с b_i = 0 для i > n с периодом 1. Если α - рациональное число, то соответствующая ему дробь (2) является периодической. Для иррационального числа α дробь (2) не является периодической.

Отрицательные числа также представляются в виде десятичных дробей, перед которыми ставится знак минус.

Десятичная  дробь применялись уже в 14-15 веках. Узбекский учёный аль-Каши описал систему десятичных дробей в 1427 году. В Европе десятичную дробь ввёл в употребление С. Стевин (1584). В русской литературе учение о десятичных дробях первым изложил Л.Ф. Магницкий в «Арифметике» (1703). С помощью бесконечных десятичных дробей К. Вейерштрассом во 2-й половине 19 века была построена одна из строгих теорий действительных чисел.

Лит.: Нивен А. Числа рациональные и иррациональные. М., 1966.