Дифференциальное уравнение обыкновенное

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ обыкновенное, уравнение, содержащее искомую функцию одной независимой переменной, её производные различных порядков и саму независимую переменную. Точнее, обыкновенным дифференциальным уравнением называется уравнение вида (1)

относительно функции х(t) переменной t, где Ф - известная функция от n + 2 переменных, а х’, х", ..., х(n) обозначают производные функции х соответствующих порядков. Такое уравнение называется обыкновенным дифференциальным уравнением n-го порядка. Эти уравнения называют обыкновенными дифференциальными уравнениями с тем, чтобы отличить их от дифференциальных уравнений с частными производными. Как для самой функции х, так и для процесса нахождения этой функции используется термин «решение дифференциального уравнения» (иногда процесс нахождения решения называют «интегрированием дифференциального уравнения»). Говорят, что дифференциальное уравнение n-го порядка (1) является разрешённым относительно старшей производной, если оно записано в виде (2)

Простейшие дифференциальные уравнения появились в работах И. Ньютона: задача о нахождении первообразной (неопределённого интеграла) х(t) для данной функции f(t) эквивалентна решению уравнения х’(t) = f(t). Термин «дифференциальное уравнение» предложил Г. В. Лейбниц (1676).

Пример обыкновенного дифференциальное уравнения даёт 2-й закон Ньютона, описывающий движение по прямой материальной точки под действием внешней силы. Если m - масса точки, х(t) - её текущая, изменяющаяся во времени t координата на прямой, а F - приложенная к точке сила (зависящая, вообще говоря, от времени, положения точки и её скорости), то закон  движения  х(t)  определяется  дифференциальным уравнением

mx’’ = F(t, x, x’) (3)

Простейшее дифференциальное уравнение х’ = 0, которое обращает в тождество любая постоянная функция х(t) = С, показывает, что дифференциальное уравнение (2), вообще говоря, имеет бесконечно много решений. Вся совокупность решений дифференциального уравнения (2), как правило, может быть записана в виде функции х =  х (t, С₁, ... , C_n), содержащей n параметров (так называемых произвольных постоянных) С₁, ... , C_n и называемой общим решением дифференциального уравнения. При любом конкретном выборе числовых значений этих n параметров получается  так называемое  частное  решение  дифференциального уравнения (2). Например, уравнению гармонических колебаний х" + ω²х = 0, где ω - заданное положительное число, удовлетворяет любая функция х(t) = Asin(ωt + φ), описывающая периодические колебания по времени t с периодом φ и произвольными амплитудой А и фазой φ, играющими роль произвольных постоянных.

Иногда  общее  решение  любого  дифференциального уравнения (2) удаётся записать с помощью явной зависимости от t, содержащей алгебраические операции, элементарные функции и n произвольных постоянных. Так, известно, что общее решение так называемого линейного дифференциального уравнения n-го порядка

с постоянными коэффициентами α ≠ 0, α _n-1, ..., α₁, α₀  имеет  вид

где λ1, λ2, ..., λn - корни характеристического уравнения α_nλ_n + α_n-1λ_n-1 + ... + α₁λ + α₀ = 0. Однако такие формулы удаётся получить лишь в исключительных случаях. Это связано с тем, что набор элементарных функций является недостаточным для этих целей. Более того, в связи с дифференциальным уравнением появились новые функции, которые, в отличие от элементарных, называют специальными функциями.

Поскольку дифференциальное уравнение (2) имеет бесконечное множество решений, можно искать его решения, подчинённые одновременно дополнительным условиям. Особенно важны такие дополнительные условия, при выполнении которых выделяется единственное решение дифференциального уравнения (2).

Начальной задачей (Коши задачей) для дифференциального уравнения (2) называется задача отыскания функции х(t), удовлетворяющей, помимо дифференциального уравнения (2), набору начальных условий (4)

где t₀ - фиксированное начальное значение аргумента t, а, а₀, а₁, а₂, ... , a_n-1 - заданные числа (начальные значения). Если f - всюду определённая дифференцируемая функция n + 1 переменных, то задача Коши (2), (4) при любом начальном значении аргумента и любых начальных значениях однозначно разрешима, т. е. имеет, и притом единственное, решение. Для  2-го  закона  Ньютона (3) это означает, что если в начальный момент времени t₀ заданы исходное положение точки х(t₀) и её начальная скорость х’(t₀), то движение точки х(t) определяется однозначно.

Общее решение дифференциального уравнения первого порядка

x’ = f(t, x) (5)

где функция f определена и дифференцируема на всей плоскости (t, х), геометрически представляется однопараметрическим семейством гладких кривых х = х(t, С), где С - произвольная числовая постоянная, которые без самопересечений и взаимопересечений покрывают всю плоскость. Так, общим решением уравнения  экспоненциального роста х’ = λх является семейство х = Сехр(λt).  Другими словами, через каждую точку (t₀, х₀) плоскости проходит, и притом единственная, интегральная кривая - график решения дифференциального уравнение (5) с начальным условием х (t₀) = х₀ это частное решение соответствует значению параметра С, определяемому из соотношения х₀ = х(t₀,С). Любая интегральная кривая х=х(t) дифференциального уравнения (5) в произвольной точке (t, х(t)) имеет касательную, угловой коэффициент которой равен f (t, х(t)).

К дифференциальному уравнению (2) можно присоединять и иного вида дополнительные условия, в которых, например, участвуют, в отличие от начальных условий (4), значения неизвестной функции х(t) при различных значениях аргумента. Таковы, например, краевые условия

где t₁, t₂, ..., t_n - заданные значения аргумента, а а₁, а₂, ... , а_п - фиксированные числа, или

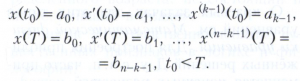
Отыскание решения дифференциального уравнения (2), удовлетворяющего некоторым краевым условиям подобного типа, называют краевой задачей для дифференциального уравнения (2). Например, ответ на вопрос, может ли материальная точка, движущаяся согласно закону Ньютона по прямой, в заранее предписанные моменты времени t₀ и Т оказаться в фиксированных положениях х₀ и х_Т на этой прямой, сводится к выяснению существования решения уравнения (3) с краевыми условиями

x(t₀) = x₀, x(_T) = x_T  (6)

т. е.  к разрешимости  краевой задачи (3), (6). Ответ на вопрос о существовании решения краевой задачи часто вызывает серьёзные трудности.

Наряду с дифференциальным уравнением вида (2) рассматриваются системы обыкновенных дифференциальных уравнений (7)

Здесь у₁, у₂, ..., y_n неизвестные функции одного и того же аргумента t, а f₁, f₂, … f_n - заданные функции n + 1 аргумента. Такая система называется системой n-го порядка. Решением системы дифференциального уравнения (7) является любая совокупность n функций у₁(t), у₂(t), ..., y_n(t) аргумента t, обращающих одновременно все соотношения  (7) в  тождества.  Если  ввести вектор y = (y₁, y₂, … y_n) и вектор-функцию f(t,y) = (f₁(t,y), f₂(t,y), … f_n(t,y)) то систему дифференциальных уравнений (7) можно записать в  векторной форме (8)

её  решением  будет вектор-функция  у = y(t) = (y₁(t), y₂(t),… y_n(t)). Общее решение системы дифференциальных уравнений (8) - вектор-функция у = у(t,С₁,...,С_n), содержащая n произвольных постоянных С₁,...,С_n. Каждое частное решение дифференциальных уравнений (8) можно интерпретировать как кривую в (n + 1)- мерном  пространстве  (t, у₁, у₂, ..., y_n).

Часто рассматриваются линейные системы дифференциальных уравнений, которые в векторной форме записываются в виде

(здесь А(t) - заданная n х n матрица, элементами которой являются функции, F(t) - известная n-мерная вектор-функция), и автономные системы дифференциальных уравнений - системы вида (7), для которых правые части  не зависят явно от переменной t.

Начальная задача (задача Коши) для системы дифференциальных уравнений (7) заключается в отыскании такого её решения, которое дополнительно удовлетворяет набору начальных условий (9)

где t₀ - фиксированное начальное значение аргумента, а (а₁, а₂, ..., а_n) - набор заданных чисел (начальное значение решения). Если все входящие в систему (7) функции f₁, f₂, ... , f_n всюду определены и дифференцируемы, то задача Коши (7), (9) однозначно разрешима, т. е. имеет единственное решение. Для системы дифференциальных уравнений (7) можно ставить и краевые задачи, в которых дополнительные условия накладываются на значения неизвестных функций при разных значениях независимой переменной.

Если при решении любого дифференциального уравнения (2) ввести новые неизвестные функции переменной t

то оно сводится к системе дифференциальных уравнений (7) частного вида

Поскольку решения уравнения (2) или системы (7) обычно невозможно записать явно с помощью известных функций, возникает проблема выявления свойств решений дифференциальных уравнений (периодичности, ограниченности, положительности, колеблемости, монотонности, поведения при неограниченном росте аргумента и т. д.) без знания представлений решений в виде формул, непосредственно на основе анализа только правых частей этих дифференциальных уравнений. Такими вопросами занимается качественная теория дифференциальных уравнений, основоположником которой был А. Пуанкаре.

Фундаментальным и практически значимым разделом дифференциальных уравнений является теория устойчивости, ведущая своё начало от работ А. М. Ляпунова. Пусть изучение конкретной проблемы приводит к «эталонной» задаче Коши (7), (9), решение у(t) которой определено на бесконечном промежутке времени t ≥ t₀. В прикладных проблемах (например, в задачах управления движением) как начальные значения (9) решения, так и правые части уравнений (7) принципиально не могут быть указаны абсолютно точно, малые погрешности (возмущения) в их определении неизбежны, поэтому «реальное» решение у*(t) будет отличаться от решения «эталонной» задачи и возникает вопрос, как влияют малые возмущения в данных задачи Коши на отклонение «реальных» решений у*(t) от эталонного решения у(t). Если малые возмущения начальных значений (9) приводят к малым отклонениям любого «реального» решения у*(t) от решения у(t) при всех t ≥ t₀, то решение у(t) называется устойчивым по Ляпунову и его можно (с достаточной степенью точности) использовать в качестве «эталонного» решения рассматриваемой практической задачи. В механике, физике, технике широко используются условия, обеспечивающие устойчивость по Ляпунову положений равновесия или стационарных режимов. Если малые погрешности в правых частях уравнений (7) приводят к малым отклонениям любого «реального» решения у*(t) от решения у(t) при всех t ≥ t₀, то решение у(t) называется устойчивым при постоянно действующих возмущениях. Такое решение можно использовать в качестве «эталонного» в задаче, когда, например, не удаётся учесть флуктуации сил, действующих на движущееся тело.

Любой реальный объект имеет специфические характеристики, которые описываются определёнными параметрами. Поэтому в его математическую модель должен  входить  (векторный) параметр ε = (ε₁, ... , ε_k),  так  что  вместо  системы дифференциальных уравнений (8) следует рассматривать систему у’ = f (t, у, ε). Значения этих параметров могут быть известны неточно, и возникает вопрос о нахождении условий, обеспечивающих устойчивость решений по отношению к малым возмущениям параметров. Более общий характер имеет задача выяснения зависимости решений от изменения параметров и, в частности, нахождения так называемых бифуркационных значений параметров, при прохождении которых кардинально меняются свойства решений. Иногда уравнение у’ = f (t, у, ε) имеет простое решение при ε = 0. В этом случае для решения уравнения при малых ε≠0 используются асимптотические методы, в частности возмущений теория.

В реальных прикладных, прежде всего технических, вопросах часто важна не только качественная, но и количественная информация о решении дифференциальных уравнений, нужно знать (с достаточной точностью) значения решения при различных значениях аргумента. Поэтому большое внимание уделяется численным методам решения дифференциальных уравнений.

Обыкновенные дифференциальные уравнения допускают разнообразные обобщения. В дифференциальном уравнении (5) предполагается, что значения функции х(t) и её  производной  х’(t) берутся при одном и том же значении t. Уравнение х’(t) = f (t, t - τ, х(t), х (t - τ)),  где  присутствуют значения неизвестной функции при различных значениях аргумента t и t - τ, τ ≠ 0, называется дифференциальным уравнением с отклоняющимся аргументом. Задачами изучения дифференциального уравнения х’ = f (t, х, u), где u - так называемый управляющий параметр, в качестве которого выбираются функции u = u(t), подчинённые различным условиям, занимается теория систем управления. Интенсивно развивается возникшая на базе обыкновенных дифференциальных уравнений теория динамических систем. Аналитическая теория обыкновенных дифференциальных уравнений изучает свойства решений в случае, когда в уравнении (2) участвуют комплексные функции комплексного переменного. К функциональному анализу примыкает так называемая теория абстрактных обыкновенных дифференциальных уравнений.

Практическое значение дифференциальных уравнений состоит в том, что часто объективные законы в естествознании, социально-экономических науках и технике удаётся записать в форме дифференциальных уравнений и эти уравнения, таким образом, оказываются адекватным средством для количественного описания этих законов. Например, вычисление траекторий космических полётов осуществляется путём изучения и решения дифференциальных уравнений. Хорошо известно предсказание Дж. К. Адамса (1843-45) и У. Леверье (1846) существования планеты Нептун, осуществлённое с помощью дифференциальных уравнений и лишь затем подтверждённое прямыми астрономическими наблюдениями немецкого астронома И. Галле (1846).

Лит.: Хартман Ф. Обыкновенные дифференциальные уравнения. М., 1970; Эрроусмит Д. К., Плейс К. М. Обыкновенные дифференциальные уравнения. М., 1986; Понтрягин Л. С. Обыкновенные дифференциальные уравнения. 6-е изд. М.; Ижевск, 2001; Боровских А. В., Перов А. И. Лекции по обыкновенным дифференциальным уравнениям. М.; Ижевск, 2004.