Дисперсионный анализ в матема­тике

ДИСПЕРСИОННЫЙ АНАЛИЗ в математике, статистический метод, предназначенный для выявления влияния отдельных факторов на результат эксперимента, а также для последующего планирования экспериментов.

Если значения неизвестных постоянных а₁,..., a_I  могут  быть  измерены с помощью различных методов или измерительных средств М₁,..., M_J и в каждом случае так называемая систематическая ошибка b_ij может, вообще говоря, зависеть как от выбранного метода M_j, так и от неизвестного измеряемого значения a_i , то результаты таких измерений представляют собой суммы вида

x_ijk = a_i + b_ij + y_ijk,

i = 1, ... , I,  j = 1, ... , J,  k = 1, ... , К,

где К - число независимых измерений неизвестной величины a_i - методом M_j, а y_ijk - случайная ошибка k-го измерения величины a_i методом M_j. При этом предполагается, что все y_ijk - независимые одинаково распределённые случайные величины, имеющие нулевое математическое ожидание. Такая линейная модель называется двухфакторной схемой дисперсионного анализа; первый фактор - истинное значение измеряемой величины, второй - метод измерения, причём в данном случае для каждой возможной комбинации значений первого и второго факторов осуществляется одинаковое число К независимых измерений (в более сложных моделях дисперсионного анализа от последнего предположения иногда отказываются).

Например, пусть в соревнованиях участвуют I спортсменов, мастерство которых оценивается J судьями, причём каждый участник соревнований выступает К раз (имеет К попыток). В этом случае a_i - истинное значение показателя мастерства спортсмена с номером i, b_ij - систематическая ошибка, вносимая в оценку мастерства i-го спортсмена судьёй с номером j, x_ijk - оценка, выставленная j-м судьёй i-му спортсмену за k-ю попытку, а y_ijk- случайная погрешность. Подобная схема типична для так называемой субъективной экспертизы качества нескольких объектов, осуществляемой группой экспертов. Другой пример - статистическое исследование урожайности сельскохозяйственной культуры в зависимости от одного из I сортов почвы и J методов её обработки, причём для каждого сорта почвы i и каждого метода обработки с номером j осуществляется К независимых экспериментов. В этом примере можно считать, что величины a_i равны нулю, b_ij - истинное значение урожайности для i-го сорта почвы при j-м методе обработки, x_ijk - соответствующая экспериментально наблюдаемая урожайность в k-м опыте, а y_ijk - её случайная ошибка, возникающая из-за тех или иных случайных причин.

Пусть

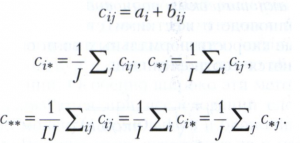
Пусть, кроме  того,

Идея дисперсионного анализа  основана  на тождествах

i = 1, ... , I,  j = 1, ... , J.

В примере, связанном со спортивными соревнованиями, функция δ_ij выражает отношение j-го судьи к i-му спортсмену (положительное значение δ_ij означает подсуживание, т. е. систематическое завышение j-м судьёй оценки мастерства i-го спортсмена, а отрицательное значение δ_ij - засуживание, т. е. систематическое снижение оценки). Равенство всех δ_ij нулю - обычное требование, которое предъявляют к работе группы экспертов. В случае агрономических опытов такое равенство рассматривается как гипотеза, подлежащая проверке по результатам экспериментов. Если эта гипотеза верна, то выявление наилучших почвы и обработки может быть осуществлено раздельно, что приводит к существенному сокращению числа экспериментов.

В ситуации спортивных соревнований функция γ_j может трактоваться как систематическая ошибка, допускаемая j-м судьёй по отношению ко всем спортсменам, т. е. γ_j - характеристика строгости или либеральности j-го судьи. В реальных условиях γ_j могут иметь ненулевые значения, что  приходится  учитывать  при подведении итогов экспертизы. Сумма двух оставшихся функций α + β_i зависит лишь от i и поэтому может быть использована для оценки мастерства i-го спортсмена. Однако следует учитывать, что величина α + β_i ≠ a_i оценивает не только мастерство i-го спортсмена, но в той или иной мере отношение экспертов к его мастерству.

Истинные значения функций α, β_i, γ_j и δ_ij неизвестны и выражаются в терминах неизвестных функций c_ij. Поэтому первый этап дисперсионного анализа заключается в отыскании статистических оценок для c_ij по результатам наблюдений x_ijk. Несмещённая и имеющая минимальную дисперсию оценка для c_ij выражается формулой

Несмещённые оценки

для функций  α, β_i, γ_j, δ_ij,  имеющие   минимальные дисперсии, получаются в результате замены аргументов c_ij соответствующими  оценками

На основе этих оценок строится второй этап дисперсионного анализа, посвящённый выявлению влияния первого и второго факторов на результаты эксперимента (в агрономических опытах первый фактор - сорт почвы, второй - метод обработки). Статистическими методами проверяется гипотеза отсутствия   взаимодействия  факторов, которая соответствует  равенству

а также гипотезы

и

Дальнейшие этапы дисперсионного анализа существенно зависят не только от реального содержания конкретной задачи, но также и от результатов статистической проверки гипотез на втором этапе. Например, в условиях  агрономических  опытов  справедливость гипотезы

позволяет  более экономично спланировать дальнейшие эксперименты  (если  помимо  гипотезы

справедлива также и гипотеза

то  это означает, что урожайность зависит лишь от сорта почвы).

Справедливость гипотезы

даёт основание для упорядочивания сравниваемых  объектов (например,  спортсменов) по значениям величин

Первоначально дисперсионный анализ был предложен Р. Фишером (1925) для обработки результатов агрономических опытов по выявлению условий, при которых испытываемый сорт сельскохозяйственной культуры даёт максимальный урожай. Современные приложения дисперсионного анализа охватывают широкий круг задач экономики, социологии, биологии и техники и трактуются обычно в терминах статистической теории выявления систематических различий между результатами измерений, выполненных при тех или иных меняющихся условиях. Смотри также Математическая  статистика.

Лит.: Хальд А. Математическая статистика с техническими приложениями. М., 1956; Снедекор Дж. У. Статистические методы в применении к исследованиям в сельском хозяйстве и биологии. М., 1961; Шеффе Г. Дисперсионный анализ. 2-е изд. М., 1980.