Доверительный интервал

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ, интервал, построенный по результатам наблюдений над случайной величиной, накрывающий с заданной вероятностью неизвестное значение параметра распределения этой случайной величины. Пусть результаты наблюдений Х₁,..,Х_n суть независимые случайные величины с распределением вероятностей Р_θ, зависящим от числового параметра θ, θ ∈ Θ, где Θ – так называемое параметрическое множество. Тогда при фиксированном α, 0 < α < 1, интервал с границами

И

лежащий в множестве Θ такой, что

где нижняя грань берется по θ ∈ Θ называется доверительным интервалом для параметра  θ  с доверительным уровнем (коэффициентом доверия) 1-α. Границы   и    доверительного интервала называются доверительными границами или доверительными пределами.

Пример. Пусть  Р_θ – нормальное распределение с плотностью вероятности

где -∞ < х < ∞ и ς - известное положительное число. При построении доверительного интервала для параметра θ рассматриваются статистическая  оценка

параметра θ и случайная величина

которая при любом значении  θ  имеет  функцию  распределения

стандартного  нормального  закона.  Поэтому  для  любого t > 0 вероятность

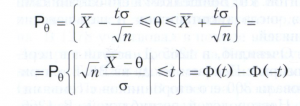
не зависит от θ. Пусть t_α - решение уравнения 2Ф(t_α) - 1 = 1 - α, где 0 < α < 1. Интервал

накрывает неизвестное значение θ с вероятностью 1 - α, т. е. является доверительным интервалом с доверительным уровнем 1 - α. Вероятность ошибки, состоящей в том, что построенный доверительный интервал  не накрывает истинное значение θ, не превосходит α.

Понятие доверительного интервала обобщается на случай векторного параметра, при этом используются многомерные доверительные области. Понятие доверительного интервала обобщается и на функциональные характеристики вероятностных распределений. Задача построения наилучших доверительных интервалов родственна задаче получения наилучших критериев в теории статистических гипотез проверки.

Метод оценивания параметров с помощью доверительных интервалов предложен американским математиком Е. Нейманом (1935). Понятие доверительного интервала широко используется при статистической обработке результатов наблюдений.

Лит.: Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. 3-е изд. М., 1983; Крамер Г. Математические методы статистики. 2-е изд. М., 2003.