Гамильтона уравнения

ГАМИЛЬТОНА УРАВНЕНИЯ (канонические уравнения механики), дифференциальные уравнения движения голономных механических систем, находящихся под действием потенциальных сил. Предложены У. Гамильтоном в 1834 году.

Гамильтона уравнения эквивалентны Лагранжа уравнениям 2-го рода, в которых неизвестными являются обобщённые координаты q_i и обобщённые скорости ?_i= dq_i/dt (t - время). Вместо переменных ?_i Гамильтон ввёл в рассмотрение обобщённые импульсы p_i = дL/д?_i [i = 1, ..., n, L(t, q_i, ?_it) - функция Лагранжа, n - число степеней свободы системы], а также функцию Н(t, q_i, p_i), называемую Гамильтона функцией.

Гамильтона уравнения имеют вид

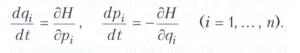
Гамильтона уравнения представляют собой систему 2n обыкновенных дифференциальных уравнений 1-го порядка, интегрируя которые, можно найти все неизвестные q_i и p_i как функции времени t, а из начальных условий - 2n постоянных интегрирования. Решение системы Гамильтона уравнения можно также свести к отысканию полного интеграла соответствующего ей уравнения в частных производных (Гамильтона-Якоби уравнения).

Если гамильтониан не зависит от времени (дН/дt = 0), то Гамильтона уравнения допускают интеграл Н = h = const (в классической механике ему соответствует интеграл энергии). Если гамильтониан не зависит от какой-либо обобщённой координаты q_s (дН/дq_s = 0), то Гамильтона уравнения допускают интеграл p_s = c_s = const (координата q_s называется циклической, а соответствующий ей интеграл - циклическим интегралом).

Гамильтона уравнения имеют простую и симметричную структуру, они применяются при исследовании теоретических проблем аналитической механики и классического вариационного исчисления. Свойства Гамильтона уравнения лежат в основе современной теории возмущений и используются в статистической физике, квантовой механике и других областях физики. Гамильтона уравнения применяются также при решении задач теории оптимального управления на основе принципа максимума Понтрягина.

А. В. Карапетян.