Гамильтона функция
ГАМИЛЬТОНА ФУНКЦИЯ, функция, введённая У. Гамильтоном для описания движений голономных механических систем, находящихся под действием потенциальных сил, выраженная через обобщённые координаты и обобщённые импульсы. (В квантовой механике Гамильтона функции соответствует оператор Гамильтона - гамильтониан.)
Пусть q1 ,.., qn и ?i ,..., ?n - обобщённые координаты и обобщённые скорости голономной механической системы с n степенями свободы и L=L(t, qi, ?i) - функция Лагранжа (t - время). В классической механике L = Т - П, где Т - кинетическая и П - потенциальная энергии соответственно. Обобщённые импульсы Pi вводятся при помощи соотношений
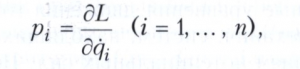
которые в классической механике всегда разрешимы относительно обобщённых скоростей
![]()
Гамильтона функция определяется соотношением
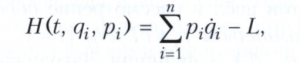
Реклама
в правой части которого величины ?i выражены формулой (1).
Если функция Н не зависит явно от времени, то она сохраняет постоянное значение во всё время движения:
Н(qi, pi) = const. (2)
В частности, если связи, наложенные на систему, стационарны, то Гамильтона функция совпадает с полной механической энергией системы Н = Т + П, выраженной через qi, pi , В этом случае соотношение (2) представляет собой интеграл энергии.
Гамильтона функция Н, как и функция Лагранжа L, полностью характеризует голономную консервативную механическую систему. При помощи Гамильтона функции уравнения движения системы могут быть записаны в виде системы 2n обыкновенных дифференциальных уравнений 1-го порядка (смотри Гамильтона уравнения). Через Гамильтона функции записывается Гамильтона-Якоби уравнение. Гамильтона функция используется в задачах оптимального управления, а также обобщается на системы с бесконечным числом степеней свободы.
А. В. Карапетян.