Инвариантов теория

ИНВАРИАНТОВ ТЕОРИЯ, алгебраическая теория, изучающая многочлены или, более общо, рациональные функции, не изменяющиеся (или изменяющиеся определённым образом) при невырожденных линейных заменах переменных. При этом, вообще говоря, рассматриваются не все такие замены, а некоторая их группа, указанные многочлены (более общо, рациональные функции) называются инвариантами этой группы.

Например, так называемая бинарная форма 2-й степени f = ах² + 2bху + су² от переменных х и у с буквенными коэффициентами а, b, с при замене х на αх + βу, у на ух + δу, где α, β, γ, δ - числа, преобразуется в бинарную форму а̅х² + 2b̅xy + с̅у², где

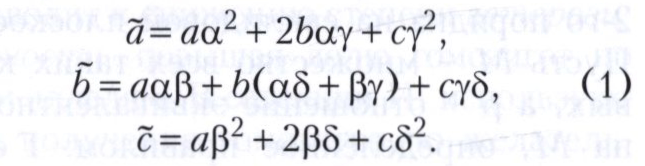
Если указанная замена переменных унимодулярна, т. е. αδ - δγ = 1, то справедливо равенство ac-b² = а̅с̅-b̅². В этом случае говорят, что многочлен ас - b² от коэффициентов бинарной формы f (дискриминант) является её унимодулярным инвариантом. Для любой указанной невырожденной замены переменных, то есть такой, что αδ-βγ ≠ 0, из (1) следует равенство (ас - b²)/(а + с)² = (а̅с̅ - b̅²)/(а̅+с̅)². В этом случае говорят, что рациональная функция (ас-b²)/(а + с)² от коэффициентов бинарной формы f является её абсолютным инвариантом. Аналогично определяются инварианты форм любых степеней от любого числа переменных и, более общо, инварианты конечной системы таких форм. Например, многочлен 3b²с² + 6abcd + 4ас³ - а²d² - унимодулярный инвариант бинарной формы 3-й степени ах³ + 3bx²у + + 3cxy² + dy³ от переменных х и у, а ad-bc - унимодулярный инвариант системы из двух бинарных форм 1-й степени αх + by и cx + dy.

Инвариантов теория возникла под влиянием ряда задач теории чисел, алгебры и геометрии. К. Гаусс поставил задачу изучения многочленов от коэффициентов бинарной формы ах² + 2bxy + су², не меняющихся при преобразованиях этих коэффициентов, определяемых унимодулярными заменами переменных при целых а, р, у и δ. В проективной геометрии появляются алгебраические выражения от проективных координат, не меняющиеся при проективных преобразованиях, например двойное отношение упорядоченного набора четырёх точек проективной прямой. Арифметическими и алгебраическими вопросами, так или иначе связанными с инвариантов теорией, занимались К. Якоби, немецкий математик Ф. Эйзенштейн, Ш. Эрмит. Как математическая дисциплина инвариантов теория сложилась к середине 19 века. К этому времени понятия группы, инварианта и основные задачи инвариантов теории были строго сформулированы и стало ясно, что многие факты классической и проективной геометрий суть выражение тождеств (сизигий) между инвариантами соответствующей группы преобразований. Первой работой по инвариантов теории является, по-видимому, «Мемуар о гипердетерминантах» А. Кэли (1846). Все классические термины инвариантов теории - инвариант, ковариант, дискриминант, сизигия и т. д. - были введены Дж. Сильвестром.

В 19 веке основным объектом изучения инвариантов теории были унимодулярные инварианты форм, и основная задача инвариантов теории состояла в описании всех инвариантов. С этой целью были разработаны различные формальные процедуры, создан так называемый символический метод - формальный способ вычислять все инварианты степени не выше заданной. В процессе развития классической инвариантов теории главные усилия исследователей стали сосредоточиваться вокруг решения двух основных проблем.

Первая из них формулируется следующим образом. Рассматриваются унимодулярные инварианты некоторой системы форм. Требуется доказать существование такой конечной системы F₁,..., F_d этих инвариантов, что любой инвариант F выражается через F₁,..., F_d с помощью операции сложения и умножения, т. е. представляется в виде многочлена от F₁,...,F_d. Вообще говоря, F₁ , ... , F_d не независимы: могут существовать ненулевые многочлены Р от переменных t₁t_d, называемые сизигиями, которые после подстановки t₁ = F_i, i = 1,...d, тождественно обращаются в нуль.

Вторая основная проблема состоит в доказательстве существования конечного набора так называемых базисных сизигий, алгебраическими следствиями которых являются все остальные. Обе основные проблемы были положительно решены Д. Гильбертом, 1-я в 1890, а 2-я в 1893 году. Его доказательства основывались на общих абстрактных алгебраических утверждениях, составивших позднее фундамент современной коммутативной алгебры. Подход Гильберта не даёт принципиального способа найти F₁, ..., F_d. Конструктивное доказательство было найдено российским математиком В. Л. Поповым (1981).

Развившаяся к 1930-м годам теория групп Ли и их представлений привела к следующей геометрической переформулировке задач инвариантов теории. Задано линейное действие группы G в конечномерном линейном пространстве V. Инварианты этого действия - многочлены на V, постоянные на орбитах группы G, и цель инвариантов теории - их описание. В 1930-х годах Г. Вейль распространил решение Гильберта 1-й основной проблемы на случай, когда G - компактная группа Ли или комплексная полупростая группа Ли (на эти случаи обобщается и результат Гильберта по 2-й основной проблеме). Вместе с тем японский математик М. Нагата (1958) нашёл пример, для которого 1-я основная проблема решается отрицательно. Это дало решение так называемой 14-й проблемы Гильберта.

Новый этап развития инвариантов теории связан с расширением круга задач и геометрических приложений. Современная инвариантов теория стала частью общей теории алгебраических групп преобразований, в которой исследуются разнообразные аспекты действий алгебраических групп на алгебраических многообразиях. Фундаментом этих исследований является теория алгебраических групп и их представлений, построенная в 1950-х годах, а языком - язык алгебраической геометрии.

Понятие инварианта в инвариантов теории - частный случай общематематического понятия инварианта. Под последним понимается любое отображение φ рассматриваемой совокупности М математических объектов, снабжённой некоторым отношением эквивалентности р, в другую совокупность N математических объектов, постоянное на классах эквивалентности М по р.

В случае когда классы эквивалентности отношения р являются орбитами некоторой группы G, действующей на М, инварианты р называют инвариантами группы преобразований G. Такие инварианты лежат в основе систематизации геометрических дисциплин по группам преобразований. Эта концепция была выдвинута Ф. Клейном в так называемой эрлангенской программе. Согласно этой концепции, всякая группа преобразований может служить группой преобразований систем координат в некоторой геометрии; величины, определяемые объектами этой геометрии и не меняющиеся при смене координат (инварианты), описывают внутренние свойства рассматриваемой геометрии и дают структурную классификацию её теорем. Так, например, задача проективной геометрии - нахождение инвариантов (и соотношений между ними) для проективной группы, евклидовой геометрии - для группы движений евклидова пространства, и т. д.

Общее понятие инварианта, однако, является более широким и не может быть ограничено рамками инвариантов групп преобразований. Примеры можно указать во многих областях математики. Так, кривизна поверхности, определяемая в дифференциальной геометрии, является инвариантом изгибания.

Лит.: Hilbert D. Über die Theorie der algebraischen Formen // Mathematische Annalen. 1890. Bd 36. S. 473-531; idem. Über die vollen Inva riantensysteme // Ibid. 1893. Bd 42. S. 313-373; Вейль Г. Классические группы, их инварианты и представления. М., 1947; Nagata М. On the fourteenth problem of Hilbert // Proceedings of the International congress of mathematicians (Edinburgh, 1958). Camb., 1960; Popov V.L. Constructive invariant theory // Astérisque. 1981. Vol. 87/88. Р. 303-334; Винберг Э. Б., Попов В. Л. Теория инвариантов // Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. М., 1989. Т. 55; Mumford D., Fogarty J., Kirwan F. Geometric invariant theory. 3rd ed. В.; N. Y., 1994; Derksen Н., Kemper G. Computational invariant theory. В. а. о., 2002.