Кеплера законы

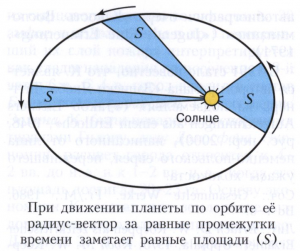
КЕПЛЕРА ЗАКОНЫ, эмпирические законы движения планет, выведенные в начале 17 века И. Кеплером в соответствии с системой мира, предложенной Н. Коперником. Основой для Кеплера законов послужили многолетние и самые точные для своего времени астрономические наблюдения за движением планет, проведённые Т. Браге. Первый Кеплера закон (так называемый закон эллипсов): орбитой каждой планеты Солнечной системы является эллипс, в одном из фокусов которого располагается Солнце; второй Кеплера закон (так называемый закон площадей): радиус-вектор планеты за равные промежутки времени заметает равные площади (рис.). Третий Кеплера закон (так называемый гармонический закон): квадраты периодов обращения (Т₁ и Т₂) двух планет относятся как кубы их средних расстояний от Солнца (а₁ и а₂): Т²₁ / Т²₂ = а³₁ /а³₂. Первые два закона Кеплер опубликовал в книге «Новая астрономия» (1609), третий - в книге «Гармония Мира» (1619). С помощью открытых им законов, Кеплер в 1627 году составил «Рудольфовы таблицы» (названные в честь императора Рудольфа II Габсбурга) положения планет, которые оказались значительно точнее любых других таблиц, опиравшихся на геоцентрическую систему мира. Поэтому таблицы Кеплера в течение двух столетий использовались в практической астрономии.

Кеплера законы справедливы на таких временных интервалах, на которых влияние масс планет пренебрежимо мало в сравнении с массой Солнца. Кеплера законы сыграли определяющую роль в открытии И. Ньютоном закона всемирного тяготения. Ньютон обобщил Кеплера законы, получив их в качестве строгих следствий из общего решения двух тел задачи, в которой отсутствуют какие-либо ограничения на массы компонентов двойной системы.

Обобщённые Кеплера законы формулируются следующим образом. Первый Кеплера закон: в невозмущённом движении (смотри Кеплеровское движение) орбитой материальной точки является коническое сечение, в одном из фокусов которого расположен доминирующий центр притяжения. Второй Кеплера закон: в невозмущённом движении площадь конического сечения, описываемая радиус-вектором движущейся материальной точки, изменяется прямо пропорционально времени, так что секторная скорость оказывается постоянной. Третий Кеплера закон; в невозмущённом эллиптическом движении материальной точки произведение квадрата среднего движения (угловой скорости орбитального движения) на куб большой полуоси орбиты равно произведению гравитационной постоянной на суммарную массу двойной системы. Или в другой формулировке (эквивалентной предыдущей): в относительном движении двух материальных точек (вокруг центра притяжения) произведения квадратов периодов обращения на суммы масс центральной и движущейся точек (соответственно М и m) относятся как кубы больших полуосей их эллиптических орбит: Т²₁ (М + m₁)/Т²₂ (М + m₂) = а³₁ /а³₂.

Кеплера законы используют при решении ряда астрономических задач, например при определении масс компонентов двойных звёзд.

Лит.: Рябов Ю. А. Движения небесных тел. 4-е изд. М., 1988.