Корреляционный анализ

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ, раздел математической статистики, предназначенный для оценки корреляции между случайными величинами и проверки гипотез о значимости связи между ними. Корреляционный анализ статистических данных использует следующие основные практические приёмы: построение корреляционного поля и составление корреляционной таблицы; вычисление выборочных коэффициентов корреляции; проверку статистических гипотез значимости связи. Дальнейшее исследование может заключаться в установлении конкретного вида зависимости между величинами (смотри Регрессионный анализ).

Вспомогательными средствами при анализе выборочных двумерных данных являются корреляционное поле и корреляционная таблица. Корреляционное поле получают, нанося выборочные точки на координатную плоскость. По характеру расположения точек поля можно составить предварительное представление о форме зависимости случайных величин (например, о том, что одна величина в среднем возрастает или убывает при возрастании другой). Для численной обработки результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке этой таблицы приводятся численности n_ij тех пар (х,у), компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Обычно длины интервалов группировки (по каждой из переменных) выбирают равными между собой, и центры (соответственно у₁) этих интервалов, и числа n_ij используют в качестве основы для расчётов.

Корреляционная таблица позволяет, в частности, вычислить выборочный коэффициент корреляции и выборочное корреляционное отношение. Выборочный коэффициент корреляции определяется по формуле

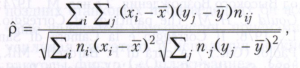
где n_i = Σ_jn_ij,   n_j = Σ_in_ij и ȳ = Σ_in_jy_j/n. При большом числе независимых наблюдений, подчинённых одному и тому же распределению, близкому к нормальному,  близок к истинному корреляции коэффициенту ρ. В других случаях в качестве характеристики связи между Х и Y рекомендуется использовать корреляционное отношение  интерпретация которого не зависит от вида исследуемой зависимости. Выборочное значение  вычисляется по данным корреляционной таблицы:

где числитель характеризует рассеяние условных средних значений  около безусловного среднего ȳ (аналогично определяется выборочное значение 

Величина используется в качестве индикатора отклонения регрессии от линейной.

Один из методов проверки гипотезы о значимости связи между Х и Y основывается на распределении выборочного коэффициента корреляции. В случае нормального распределения величина выборочного коэффициента корреляции считается значимо отличной от нуля, если выполняется неравенство

где t_α есть квантиль порядка α Стьюдента распределения с n-2 степенями свободы, соответствующая выбранному значимости уровню α. В случае ρ ≠ 0 часто используют так называемое z-преобразование Фишера, заменяя величину  на

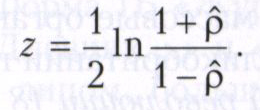
Уже при сравнительно небольших n распределение величины z хорошо приближается нормальным распределением с математическим ожиданием, равным

и дисперсией, равной 1/(n - 3). Из этого можно определить интервалы (доверительные границы) для истинного коэффициента корреляции р.

Лит.: Ван дер Варден В. Л. Математическая статистика. М., 1960; Айвазян С. А. Статистическое исследование зависимостей. М., 1968; Кендалл М., Стьюарт А. Статистические выводы и связи. М., 1973; Крамер Г. Математические методы статистики. 3-е изд. М.; Ижевск, 2003.