Лагранжа точки

ЛАГРАНЖА ТОЧКИ (точки либрации), точки в пространстве, в которых тело малой массы может находиться в относительном равновесии по отношению к двум другим небесным телам (в так называемой ограниченной задаче трёх тел).

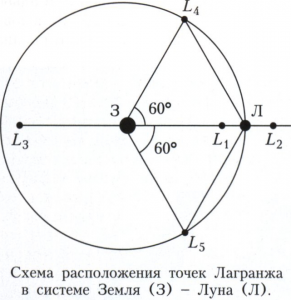
Аналитическое решение общей задачи трёх тел имеет вид абсолютно сходящихся рядов, из-за чрезвычайно медленной сходимости которых это решение для астрономических приложений практически бесполезно. Однако существуют пять строгих частных решений этой задачи, которым соответствуют движения с сохранением особых конфигураций в расположении трёх тел: тела образуют равносторонний треугольник (треугольная конфигурация) или располагаются на одной прямой (прямолинейная конфигурация). Такие же точные частные решения существуют и в ограниченной задаче трёх тел, в которой исследуется движение тела пренебрежимо малой массы в гравитационном поле двух тел конечной массы. В ограниченной круговой задаче трёх тел этим стационарным частным решениям соответствуют неподвижные точки (Лагранжа точки), лежащие в плоскости орбитального движения двух главных притягивающих тел, если рассматривается движение относительно неинерциальной барицентрической системы отсчёта, вращающейся вместе с главными притягивающими телами. Существует пять Лагранжа точек: три так называемые коллинеарные точки (L₁, L₂ и L₃, смотри рисунок) и две так называемые треугольные точки (L₄ и L₅).

В Лагранжа точках силы всемирного тяготения, действующие на тело малой массы со стороны двух главных центров притяжения, уравновешиваются центробежной силой инерции, существующей во вращающейся системе отсчёта. Тело пренебрежимо малой массы, помещённое в любую из пяти Лагранжа точек, в рассматриваемой неинерциальной системе отсчёта будет иметь нулевую скорость и нулевое ускорение.

Лагранжа точки называют также точками либрации (от латинского libro - колебаться), что обусловлено существованием в окрестности каждой из этих точек частных периодических движений по эллиптическим орбитам. В современной небесной механике не существует единообразия в наименовании точек либрации. Так, например, коллинеарные точки либрации часто называют эйлеровыми, так как впервые соответствующие им прямолинейные частные решения ограниченной задачи трёх тел были получены Л. Эйлером в 1767 году. Наименование «Лагранжа точки» принято благодаря их описанию в работе Ж. Лагранжа «О задаче трёх тел» (1772). Все пять точек либрации именуются также лапласовыми точками на том основании, что они были включены П. Лапласом в его «Трактат о небесной механике» (1798) без всяких ссылок на предшественников.

Лагранж считал открытые им точные решения задачи трёх тел «математическим курьёзом», не имеющим никакого практического приложения к реальным тройным системам небесных тел. Этот вывод был опровергнут в 1906 году, когда немецкий астроном М. Вольф обнаружил астероид Ахилл, первый из группы астероидов, расположенных в районе треугольных Лагранжа точек системы Солнце - Юпитер (смотри Троянцы в астрономии). Треугольные точки либрации иногда называют гравитационными ловушками, т.к. вблизи них могут существовать скопления частиц метеорного вещества и даже группы астероидов. На использовании динамических свойств точек либрации базируется одна из перспективных стратегий освоения межпланетного пространства. Несколько космических обсерваторий размещены в окрестностях Лагранжа точек системы Земля - Солнце [например, в районе точки L₁ - обсерватория SOHO (Solar and Heliospheric Observátory)]. Точка L₁ системы Земля - Луна рассматривается как место для размещения ретрансляционной станции на период предполагаемого освоения Луны. Предложен ряд проектов, предусматривающих создание в окрестности Лагранжа точек тел Солнечной системы спасательных станций, депо для межпланетных кораблей и даже космических мегаполисов. Понятие Лагранжа точек нашло приложение и в звёздной астрофизике: внутренняя Лагранжа точка (L₁) играет ключевую роль в теории тесных двойных звёзд.

Лит.: Справочное руководство по небесной механике и астродинамике. 2-е изд. М., 1976; Дубошин Г. Н. Небесная механика. М., 1983.