Лагранжа уравнения

ЛАГРАНЖА УРАВНЕНИЯ механики, обыкновенные дифференциальные уравнения второго порядка, описывающие движение механических систем под воздействием приложенных к ним сил. Выведены Ж. Лагранжем в 1788 в двух формах: Лагранжа уравнения 1-го рода - уравнения в декартовых координатах с неопределенными множителями Лагранжа, и Лагранжа уравнения 2-го рода - уравнения в обобщённых лагранжевых координатах.

Лагранжа уравнения 1-го рода имеют вид

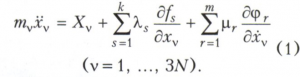
f_s(х₁, ..., х_3N, t) = 0 (s = 1, ..., k) - геометрические связи, φ_r(х₁ ..., х_3N, х₁, ..., х_3N, t) = 0 (r = 1, ..., m) – кинематические связи, накладываемые на механическую систему; N - число точек системы; t -время; k и m - число геометрических и кинематических связей соответственно; x_v - декартовы координаты (ẋ_v - скорости, ẍ_v - ускорения) точек; m_v - массы точек; Х_v - проекции на оси координат заданных активных сил; λ_s, μ_r - неопределённые множители Лагранжа, пропорциональные реакциям связей. Дифференциальные уравнения (1) вместе с k + m уравнениями связей составляют замкнутую систему уравнений относительно 3N + k + m неизвестных x_v, λ_s, μ_r. На практике Лагранжа уравнения 1-го рода применяются редко.

Лагранжа уравнения 2-го рода могут быть выведены из Д’Аламбера - Лагранжа принципа или из наименьшего действия принципа. Лагранжа уравнения 2-го рода представляют собой дифференциальные уравнения движения несвободной механической системы, на которую наложены голономные удерживающие идеальные связи (смотри Связи механические). Неизвестными величинами в этих уравнениях являются обобщённые координаты q_i (i = 1, ..., n) - независимые параметры, определяющие положение механической системы; их число n равно числу степеней свободы системы. Лагранжа уравнения 2-го рода имеют вид

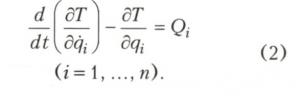
Здесь q_i - обобщённые скорости, Т - кинетическая энергия системы, Q_i - обобщённые активные силы. Если некоторые связи не являются идеальными, то соответствующие им реакции связей (силы трения) добавляют к действующим на систему активным силам. Уравнения (2) представляют собой систему n обыкновенных дифференциальных уравнений второго порядка с неизвестными функциями. Форма Лагранжа уравнения не зависит от выбора обобщённых координат. При другом выборе изменились бы только функции T и Q, а сама форма уравнений (2) осталась бы той же.

Система уравнений движения (2) имеет наименьший возможный порядок 2n. В этом, а также в отсутствии в уравнениях (2) неизвестных реакций связей состоит большое преимущество уравнений (2) по сравнению с Лагранжа уравнением 1-го рода, которое делает их удобными для практического использования. Общее решение уравнений (2) зависит от 2n произвольных постоянных (начальных условий): начальных значений обобщённых координат и обобщённых скоростей. Уравнения (2) всегда разрешимы относительно обобщённых ускорений q_i, т.к. квадратичная часть функции Т(q_i, q_i, t) является положительно определённой квадратичной формой переменных q_i. Если силы, действующие на механическую систему, потенциальны, то Q_i = ∂∏l/∂q_i (i= 1, ..., n), где ∏(q₁, ..., q_n, t) - потенциальная энергия системы. В таком случае уравнения (2) принимают вид

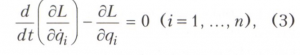
где L(q_i, q_i, t) = Т - П - Лагранжа функция.

В физике важную роль играют Лагранжа уравнения именно в форме (2), поскольку в соответствии с принципом наименьшего действия экстремальное значение действия определяется из следующего условия: функция L должна удовлетворять уравнениям (3). Лагранжа уравнения вида (3) справедливы для любой физической системы (сплошная среда, гравитационное или электромагнитное поле и др.), для которой справедлив принцип наименьшего действия.

В гидроаэродинамике Лагранжа уравнениями называют уравнения движения жидкости (газа) в переменных Лагранжа, которыми являются время t и некоторые независимые параметры a_i (i = 1, 2, 3), описывающие характеристики отдельной частицы среды (например, её декартовы координаты в некоторый начальный момент времени). Эти Лагранжа уравнения представляют собой уравнения в частных производных и имеют вид

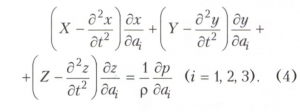
Здесь х, у, z - координаты частицы среды, Х, Y, Z - проекции объёмных сил, р - давление, ρ - плотность среды.

К уравнениям (4) следует добавить неразрывности уравнение (тоже в переменных Лагранжа) и уравнение состояния, например в виде ρ = f(р). При решении конкретных задач эту совокупность уравнений дополняют начальными и граничными условиями. Альтернативой Лагранжа уравнений являются Эйлера уравнения.

Лит.: Лагранж Ж. Аналитическая механика. М.; Л., 1950. Т. 1-2; Лурье А. И. Аналитическая механика. М., 1961; Кочин Н. Е., Кибель И. А., Розе Н. В. Теоретическая гидромеханика. 6-е изд. М., 1963. Ч. 1.