Лапласа распределение

ЛАПЛАСА РАСПРЕДЕЛЕНИЕ (двустороннее показательное распределение), распределение вероятностей случайной величины Х, заданное плотностью вероятности

где α и β, α > 0, –∞ < β < ∞, - параметры.

Лапласа распределение симметрично относительно точки х = β, имеет конечные моменты любого порядка, в частности его математическое ожидание и дисперсия равны ЕХ = β и DX = 1/α, его характеристическая функция равна

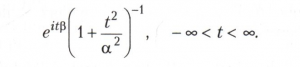
Лапласа распределение совпадает с распределением случайной величины β + Х₁ - Х₂, где Х₁ и Х₂ - независимые случайные величины, имеющие одинаковое показательное распределение с плотностью, равной 0 при х ≤ 0 и равной αе^–ах при х > 0.

Лапласа распределение введено П. Лапласом (1812) и иногда называется первым законом Лапласа, в отличие от второго закона, которым иногда называют нормальное распределение.

Лит.: Гнеденко В. В. Курс теории вероятностей. 9-е изд. М., 2007.