Вариационное исчисление

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ, раздел математики, в котором изучаются вопросы, связанные с экстремумами интегральных функционалов специального вида. В простейшем случае это функционалы вида

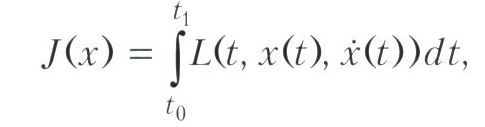
где L = L(t, х, у) - функция трёх переменных (называемая интегрантом).

Здесь х = х(t), у = у(t) - функции переменной t, t₀≤t≤t₁, ?x(t) - производная функции х(t). Таким образом, значениями аргумента функционала J являются функции х одного переменного, т. е. вариационное исчисление - раздел бесконечномерного анализа, получивший в 20 веке название функционального анализа. С другой стороны, вариационное исчисление является разделом теории экстремальных задач.

Первые задачи вариационного исчисления. Исторически первой задачей вариационного исчисления была задача о брахистохроне, состоящая в нахождении кривой наискорейшего спуска, соединяющей две заданные точки (или, иначе говоря, в нахождении формы жёлоба, соединяющего две точки, спускаясь по которому без трения под действием силы тяжести, тело завершает движение за кратчайшее время). Задачу о брахистохроне можно сформулировать как задачу вариационного исчисления о минимизации интеграла

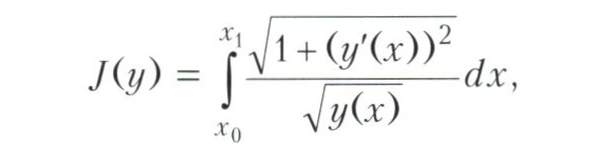
где у(х) - форма жёлоба и (х₀, у(х₀)), (х₁, у(х₁)) - закреплённые начальная и конечная точки жёлоба. Эта задача была предложена И. Бернулли в 1696 году как вызов математикам (он объявил, что знает её решение). Вызов был принят, и задача была решена крупнейшими учёными того времени - Я. Бернулли, Г. Лейбницем, французским учёным Г. Лопиталем и И. Ньютоном. Эти решения наметили многие направления будущей общей теории. И. Бернулли исходил из оптико-механической аналогии, Я. Бернулли применил принцип Гюйгенса (смотри Гюйгенса - Френеля принцип), Лейбниц решил задачу, заменяя кривую ломаными, заложив тем самым основу прямым методам в вариационном исчислении.

В вариационном исчислении можно выделить разделы, посвящённые необходимым условиям экстремума, достаточным условиям экстремума, вопросам существования экстремума и алгоритмам поиска решений.

Необходимые условия экстремума. Разделы, посвящённые необходимым условиям экстремума (и достаточным условиям экстремума), стали разрабатываться в 18 веке Л. Эйлером, Ж. Лагранжем и А. Лежандром. Начиная с 1730-х годов Эйлер занимался проблемой об условиях экстремума в задачах вариационного исчисления. Таким условием для простейших задач вариационного исчисления (простейшими называются задачи об экстремумах функционалов J при фиксированных граничных условиях) оказалась выполнимость на кривой х, подозреваемой на экстремум, дифференциального уравнения 2-го порядка

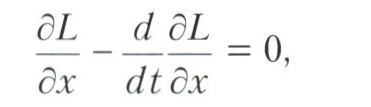
получившего название Эйлера уравнения. В важном частном случае (он связан с так называемым гармоническим осциллятором), когда L = mх² - kx², уравнение Эйлера принимает вид

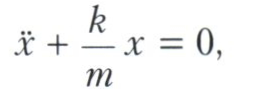
и граничные условия, вообще говоря, позволяют однозначно определить синусоиду (решение этого уравнения), соединяющую две данные точки, заданные краевыми условиями. Кривые, удовлетворяющие уравнению Эйлера, называют экстремалями, а уравнение Эйлера - условием стационарности. Это уравнение Л. Эйлер вывел прямым методом, заменяя кривую ломаной, т. е. сводя задачу к конечномерной (с последующим переходом к пределу).

Л. Эйлер стал впервые рассматривать задачи с ограничениями, а именно изопериметрические задачи, когда интеграл J минимизируется при условии, что некоторые другие интегралы принимают заданные значения. Классическая изопериметрическая задача состоит в максимизации площади, ограниченной кривой заданной длины. Разработанные Эйлером методы позволили единообразно решить ряд задач, интересных для естествознания и геометрии. Среди них задачи о провисании тяжёлой нити, о минимальной поверхности вращения, а также различные варианты классической изопериметрической задачи. Достижения вариационного исчисления приводили к пониманию того, что оно может служить языком естествознания, поскольку многие законы природы могут быть сформулированы с использованием вариационных принципов (смотри Возможных перемещений принцип, Наименьшего действия принцип).

В 1755 году задачами вариационного исчисления начал заниматься Ж. Лагранж. Он предложил новый подход к исследованию свойств экстремальных кривых, основанный на варьировании кривой, подозреваемой на экстремум, и выделении главной линейной части приращения функционала, то есть кривая, подозреваемая на экстремум, подвергается малым изменениям, варьируется, и изучается вопрос о приращении функционала, связанного с таким варьированием.

Позднее этими вопросами занимался также Л. Эйлер, который в работе «Элементы исчисления вариаций» (1764) ввёл термины «вариация» и «вариационное исчисление». Для многомерных задач вариационного исчисления методом вариаций аналоги уравнения Эйлера были получены в 1-й половине 19 века К. Гауссом и М. В. Остроградским.

Ж. Лагранж исследовал задачи вариационного исчисления с ограничениями различной природы. Для задач нахождения экстремумов функций многих переменных с ограничениями типа равенств он стал применять общий приём, получивший название метода множителей Лагранжа (смотри Лагранжа функция). Аналогичные приёмы Лагранж применял в задачах вариационного исчисления. Метод множителей Лагранжа позволяет единообразно выписывать необходимые условия экстремума в различных задачах вариационного исчисления.

Достаточные условия экстремума. Вопрос о достаточных условиях в вариационном исчислении впервые изучал И. Бернулли, но его работа (1718) оставалась неизвестной вплоть до 20 века. В 1786 году А. Лежандр нашёл необходимое условие экстремальности кривой, состоящее в том, что вторая вариация д²L/д(х?)² неотрицательна (необходимое условие Лежандра). Гипотеза о том, что достаточным условием экстремума является положительность второй вариации (усиленное условие Лежандра), оказалась неверной.

Проблему достаточности слабого экстремума (когда измеряется близость не только самих функций, но и их производных) разрешил К. Якоби, опираясь на идеи У. Гамильтона, которые тот применял для задач механики и оптики. Якоби показал, что локальных, т. е. проверяемых в отдельных точках условий (таковы уравнение Эйлера и условие Лежандра) не может быть достаточно для экстремальности кривой.

К. Якоби ввёл понятие сопряжённой точки экстремали вариационной задачи. Для простейшей задачи вариационного исчисления сопряжённая точка имеет простой геометрический смысл: это точка пересечения с экстремалью огибающей семейства экстремалей, имеющих общую начальную точку. Отсутствие сопряжённой точки на интервале от начальной до конечной точки - необходимое условие слабого минимума (необходимое условие Якоби). Отсутствие сопряжённой точки на полуинтервале от начальной точки до конечной, включая последнюю (усиленное условие Якоби), совместно с уравнением Эйлера и усиленным условием Лежандра, достаточно для слабого минимума экстремали.

В 19 веке У. Гамильтону удалось построить, отправляясь от принципа Гюйгенса, теорию оптических явлений, а К. Якоби перенёс эти концепции Гамильтона на общие задачи вариационного исчисления, что привело к созданию теории Гамильтона - Якоби. В этой теории исследуются пучки экстремалей, подобные пучкам лучей, и аналоги волновых фронтов в задачах оптики. Производящие функции, возникающие в этих задачах, удовлетворяют уравнениям с частными производными, получившим название Гамильтона - Якоби уравнений. Решение этих уравнений даёт новый подход к решению задач вариационного исчисления. При таком подходе К. Вейерштрассом в 1880-е годы были найдены условия сильного минимума (когда учитывается близость лишь фазовых координат).

Решение проблем, связанных с достаточными условиями в задачах с ограничениями, завершилось лишь к середине 20 века, когда начал складываться новый раздел теории экстремальных задач, получивший название теории оптимального управления. Задачами оптимального управления называются задачи вариационного исчисления с дополнительными условиями на переменные  (типа неравенств и включений), в которых отражаются ограниченные возможности воздействия на управляемые процессы. Фундаментальное значение в теории оптимального управления имеет Понтрягина принцип максимума; необходимые условия Эйлера, Лежандра, Якоби и Вейерштрасса являются следствиями принципа максимума.

Создание в 20 веке функционального анализа позволило рассматривать вариационное исчисление и оптимальное управление как части этого раздела математики.

Вопросы существования экстремума. Теория существования решений задач вариационного исчисления была создана в 20 веке. Основы этой теории также базируются на общих концепциях функционального анализа.

Алгоритмы поиска решения. Алгоритмы решения задач вариационного исчисления строятся на идеях штрафа, прямых методах, заменяющих задачу конечномерной, и методах решения уравнений, полученных из необходимых условий экстремума.

Лит.: Гельфанд И. М., Фомин С. В. Вариационное исчисление. М., 1961 ; Алексеев В. М., Тихомиров В. М., Фомин С. В. Оптимальное управление. М., 1979; Буслаев В. С. Лекции по вариационному исчислению. Л., 1980; Васильев Ф. П. Методы оптимизации. М., 2002.