Изопериметрическая задача
ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА, одна из классических задач вариационного исчисления. Простейшие изопериметрические задачи (нахождение треугольников и многоугольников заданного периметра, имеющих наибольшую площадь; нахождение замкнутой кривой заданной длины, ограничивающей максимальную площадь; определение замкнутой поверхности заданной площади, ограничивающей наибольший объём) были известны древнегреческим учёным. Общее изучение изопериметрических задач началось в 1696 году, когда И. Бернулли поставил задачу, состоящую в том, чтобы найти среди всех кривых, соединяющих две заданные точки, такую, для которой некоторая величина, зависящая от кривой, достигает минимума (смотри Брахистохрона). Систематическое исследование изопериметрических задач было начато Л. Эйлером в 1730-х годах.
Примером изопериметрической задачи является задача о нахождении среди кривых данной длины l, проходящих через точки А и В па плоскости, кривой у = у(х), х0 ≤ х ≤ х1 (рис.), для которой площадь криволинейной трапеции АВх1х0 максимальна.
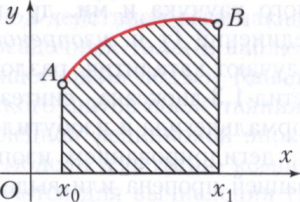
Т. к. площадь криволинейной трапеции равна
![]()
а длина дуги
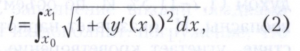
то эта изопериметрическая задача сводится к нахождению наибольшего значения интеграла (1) при заданной величине (2). Оказывается, что искомая кривая - дуга окружности.
Лит.: Лаврентьев М. А., Люстерник Л. А. Курс вариационного исчисления. 2-е изд. М.; Л., 1950; Эльсгольц Л. Э. Вариационное исчисление. 6-е изд. М., 2006.