Выпуклое программирование

ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ, раздел математического программирования, в котором исследуется задача максимизации вогнутой целевой функции f(х) векторного аргумента х = (x₁, ..., х_n), удовлетворяющего ограничениям g_i(х) ≥ 0, х Є Х, i = 1, ..., m, где g_i - вогнутые функции, Х - выпуклое множество. Точка х, удовлетворяющая этим ограничениям, называется допустимой. Основным результатом теории выпуклого программирования является теорема о седловой точке: для того чтобы допустимая точка х* задачи выпуклого программирования была оптимальной, необходимо (при довольно широких условиях) и достаточно существование вектора у* = (у*₁, ..., y_m*) с неотрицательными компонентами у* такого, что точка (х*, у*) является седловой для функции Лагранжа

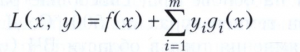
задачи выпуклого программирования, то есть для любых х Є Х и у с неотрицательными компонентами выполняются неравенства

На теорему о седловой точке опирается ряд методов выпуклого программирования, в которых либо минимизируется функция φ(y₁, ..., у_m) =  max_xЄXL(x, у) при у_i≥ 0, i = 1, ..., m, либо непосредственно отыскивается седловая точка, причём вместо функции Лагранжа иногда используются некоторые её модификации. Другой подход к решению задачи выпуклого программирования связан с поиском возможных направлений движения допустимой точки х, которые не выводят из множества допустимых точек и при движении вдоль которых целевая функция возрастает. Этот подход реализуется с помощью последовательности итераций. На каждой итерации вычисляется возможное направление, исходящее из очередной точки, после чего производится сдвиг по этому направлению на некоторое расстояние до следующей точки. Существуют методы решения задач выпуклого программирования, специально приспособленные к тому случаю, когда целевая функция нелинейна, а ограничения линейны. Как правило, методы выпуклого программирования требуют для точного определения оптимальной точки бесконечного числа итераций. Исключением являются задачи квадратичного программирования (целевая функция - сумма вогнутой квадратичной и линейной функций, ограничения линейны) и линейного программирования (целевая функция и ограничения линейны), для которых в основном используются конечные методы. Многие вычислительные методы выпуклого программирования реализованы в виде программ для ЭВМ; существуют также пакеты программ, охватывающие задачи линейного программирования и выпуклого программирования. Смотри также Исследование операций.

Лит.: Гольштейн Е. Г. Выпуклое программирование. Элементы теории. М., 1970; Зангвилл У. И. Нелинейное программирование. Единый подход. М., 1973.