Алгебраическое Число

АЛГЕБРАИЧЕСКОЕ ЧИСЛО, число а, удовлетворяющее уравнению f(х) = 0, где

n, a_n, a_n-1,.. a₁, a₀ - целые числа, n≥1, аn ≠ 0, наибольший общий делитель чисел a_n,a_n-1,...,а₁,а₀ равен единице; другими словами, f(α) = 0, т. е. а является корнем многочлена f(х). Примеры алгебраических чисел:

Любое рациональное число α = b/а, где а и b - целые числа, а≠0, является алгебраическим, так как оно - корень многочлена f(х) = ax-b. Степенью алгебраического числа α называется наименьшая из степеней всех не равных тождественно нулю многочленов с целыми коэффициентами, имеющих α своим корнем. В приведённых примерах число α₁ имеет степень 3, а числа α₂ и α₃ - степень 2. Рациональные числа и только они имеют степень 1. Действительное или комплексное число α называется трансцендентным, если оно не является алгебраическим. Т. о., трансцендентное число не может быть корнем никакого многочлена f(х) с целыми коэффициентами, f(х) ≠0. Т.к. множество всех многочленов с целыми коэффициентами счётно, то и множество алгебраических числе счётно. Множество всех действительных чисел несчётно (теорема Кантора), т. е. почти все действительные числа трансцендентны. Однако доказательство трансцендентности конкретного числа часто оказывается трудной задачей, и для доказательства трансцендентности разработаны специальные аналитические методы.

Алгебраические числа плохо приближаются рациональными числами; например, справедлива следующая теорема Лиувилля: если α действительное алгебраическое число степени n, n≥2, то существует положительное число С, зависящее только от α, такое, что при любых целых числах р и q, q> 0, выполняется неравенство:

Из этой теоремы, в частности, следует, что числа α вида

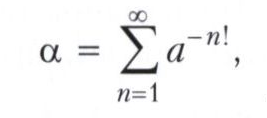
где целое число а ≥ 2 (числа Лиувилля), являются трансцендентными.

Если α – алгебраическое число степени n и, кроме того, многочлен f(х) степени n, корнем которого является α, имеет старший коэффициент a_n = 1, то α называется целым алгебраическим числом. Построена арифметика алгебраических чисел, похожая на обычную арифметику целых чисел, но имеются и принципиальные отличия от последней. В частности, в некоторых случаях в такой арифметике не выполняется теорема об однозначном разложении целых чисел на простые сомножители. Алгебраические числа находят применения в теории диофантовых уравнений.

Лит.: Гекке Э. Лекции по теории алгебраических чисел. М.; Л., 1940; Боревич З.И., Шафаревич И. Р. Теория чисел. 3-е изд. М., 1985; Галочкин А. И., Нестеренко Ю.В., Шидловский А. Б. Введение в теорию чисел. 2-е изд. М., 1995.