Булева алгебра

БУЛЕВА АЛГЕБРА (булева решётка), частично упорядоченное множество специального вида. Булеву алгебру можно формально определить как непустое множество с операциями V, Λ, ?, удовлетворяющими аксиомам:

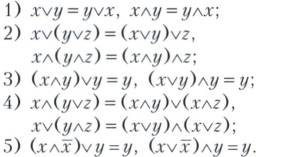
Упорядочение элементов Булевой алгебры вводится условием: ху точно тогда, когда х = хΛу. В Булевой алгебре существует наибольший элемент 1 - единица Булевой алгебры, 1=xvx?, и наименьший элемент 0 - нуль Булевой алгебры, 0 = хΛx?. Операции v и Λ называются дизъюнкцией и конъюнкцией и иногда обозначаются sup и inf, чем подчёркивается их сходство с теоретико-множественными операциями объединения и пересечения. Конъюнкция также обозначается символом &. Элемент Булевой алгебры x? называется дополнением х и иногда обозначается Сх, х’, -х, -х. Дополнение всякого элемента в Булевой алгебре единственно.

Булеву алгебру можно определить и как дистрибутивную решётку (дистрибутивную структуру; смотри Решёток теория), имеющую наибольший элемент 1 - единицу Булевой алгебры, наименьший элемент 0 - нуль Булевой алгебры и содержащую вместе с каждым своим элементом х его дополнение - элемент Сх, удовлетворяющий соотношениям

Возможны и другие аксиоматические определения Булевой алгебры. В аксиомах Булевой алгебры отражена аналогия между понятиями множества, события, высказывания. Отношение порядка в Булевой алгебре может быть (в зависимости от выбора интерпретации) истолковано как теоретико-множественное включение, как причинное следование для событий, как логическое следование для высказываний.

Кроме основных операций V, Λ, ?,  в Булевой алгебре могут быть определены и другие, среди которых особенно важна операция симметрической разности 

(пишут также х +2 у, |х-у|).

Булевы алгебры были введены Дж. Булем (1847) как аппарат символической логики. В последующем Булевы алгебры нашли широкое применение в различных разделах математики - в теории вероятностей, топологии, функциональном анализе и др. В основе приложений Булевой алгебры к логике лежит интерпретация элементов Булевой алгебры как высказываний (смотри Алгебра логики); при этом дополнение Сх истолковывается как отрицание высказывания х, а операции Λ и v - как конъюнкция и дизъюнкция высказываний. К логике близка и другая область применения Булевой алгебры - теория контактных схем. Булевы алгебры используются в аксиоматике теории вероятностей. Алгебры событий, изучаемые в теории вероятностей, суть Булевой алгебры; при этом неравенство х ≤ у означает, что событие х влечёт событие у, соответственно с этим истолковываются нуль Булевой алгебры, единица Булевой алгебры и булевы операции  V, Λ, ?. 

Примером Булевой алгебры является упорядоченная по включению система всех подмножеств фиксированного множества Q. Такая Булева алгебра обозначается 2^Q; её нулём служит пустое множество, единицей - само множество Q. Дополнение элемента х есть множество Qх; булевы операции v и Λ совпадают соответственно с объединением и пересечением.

Всякая Булева алгебра Х изоморфна некоторой алгебре множеств. Булева алгебра Х называется полной, если всякое множество Е с Х имеет верхнюю грань sup Е и нижнюю грань inf Е. Неполная Булева алгебра может быть многими способами пополнена, т. е. вложена в качестве подалгебры в некоторую полную Булеву алгебру.

Полная Булева алгебра называется нормированной, если на ней определена действительная функция μ (мера), обладающая свойствами: μ(х)>0 при Х≠0; если ЕсХ и хΛу = 0 при х,уЄЕ, х≠у, то

В теории вероятностей, где нормированные Булевы алгебры особенно важны, обычно предполагают, что μ(1) = 1. При этом значение μ(х) интерпретируется как вероятность события Х. На нормированные Булевы алгебры в основном переносится классическая теория меры и интеграла. Не всякая Булева алгебра может быть нормирована. Известны различные условия существования меры, однако они далеко не исчерпывают проблемы нормируемости.

Булева алгебра может быть наделена различными топологиями. Особенно важна так называемая (о)-топология, которая в случае нормированной Булевой алгебры метризуема и соответствует метрике

В общем случае может не существовать топологии, хорошо согласованной с порядком в булевой алгебре.

Лит.: Boole G. The mathematical analysis of logic. Camb.; L., 1847; Биркгоф Г. Теория структур. М., 1952; Halmos Р. Lectures on Boolean algebras. Toronto а. о., 1963; Kypamoвский К. Топология. М., 1969. Т. 2; Сикорский Р. Булевы алгебры. М., 1969; Владимиров Д. А. Булевы алгебры. М., 1969; Расева Е., Сикорский Р. Математика метаматематики. М., 1972.