Дифракция волн

ДИФРАКЦИЯ ВОЛН, в первоначальном узком смысле - огибание волнами препятствий; в современном, более широком - любые отклонения от законов геометрической оптики при распространении волн. При таком общем толковании дифракция волн тесно переплетается с явлениями распространения и рассеяния волн в неоднородных средах. Волны при дифракции могут попадать в область геометрической тени: огибать препятствия, стелиться вдоль поверхностей, проникать через небольшие отверстия в экранах и т.п. Например, радиоволна может проникнуть за горизонт даже без отражения от ионосферы, а звук может быть услышан за углом дома.

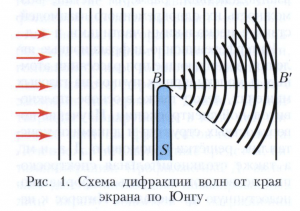
Первая волновая трактовка дифракции волн дана для света Т. Юнгом (1800), вторая - О. Френелем (1815-18). Картину волнового поля, возникающую за препятствием, Юнг считал сочетанием собственно дифракции и интерференции волн. Для объяснения дифракции волн, кроме обычных законов распространения волн в направлении лучей, он ввёл принцип поперечной передачи амплитуды колебаний непосредственно вдоль волновых фронтов (поперечной диффузии), указав, что скорость этой передачи пропорциональна длине волны и перепаду амплитуд на фронте. Согласно Юнгу, дифрагированная волна возникает локально в некоторой окрестности границы тени за краем препятствия. Аналогичная дифрагированная волна образуется и в освещённой области, так что в целом формируется поле цилиндрической волны, как бы испускаемой краем поверхности препятствия S (рисунок 1). Интерференция дифрагированной волны с не заслонённой препятствием частью падающей волны объясняет появление  на  экране В’ интерференционных полос, расположенных выше границы тени BB’, и отсутствие их в нижней части.

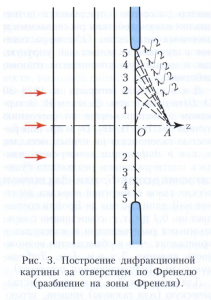
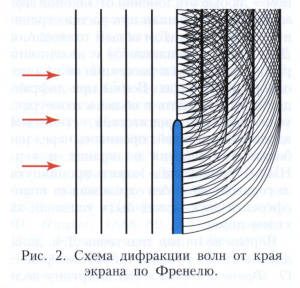О. Френель отказался от локального юнговского подхода и предложил свой интегральный метод, опирающийся на сформулированный ранее (1690) принцип Гюйгенса (смотри Гюйгенса - Френеля принцип). Согласно Френелю, дифракционное поле может быть представлено как результат интерференции полей фиктивных вторичных источников, распределённых по всей не закрытой препятствием части фронта падающей волны (рисунок 2) и имеющих амплитуду и фазу, пропорциональные таковым у этой волны. Френель разбил поверхность, занятую  вторичными  источниками, на  полуволновые зоны (так называемые Френеля зоны, рисунок 3). Характер дифракции волн зависит от того, сколько зон укладывается в отверстии, или от значения френелевского (волнового) параметра р, равного отношению размера первой зоны Френеля к радиусу а отверстия, p = √λz/a (z - координата точки наблюдения, λ - длина волны). В зависимости от величины р различают следующие области дифракции волн: геометрооптическую, или прожекторную, область, р << 1; область дифракции Френеля, р порядка 1; область дифракции Фраунгофера, р >> 1. При фиксированных а и λ эти области расположены последовательно, по мере удаления точки наблюдения от отверстия (то есть с увеличением z). В первой, прилегающей к отверстию области (z << а²/λ) поперечное распределение амплитуды повторяет распределение амплитуды на самом отверстии и отвечает приближению геометрической оптики. Во второй зоне (z порядка α²/λ) поперечное распределение амплитуды существенно искажается. Начиная с этих расстояний, волновой пучок относительно быстро расширяется из-за дифракции. В третьей, удалённой области (z >> а²/λ) дифракционное поле представляет собой расходящуюся сферическая волну с локально плоской структурой, обладающую определённой направленностью. Таким образом, наиболее отчётливо дифракция волн проявляется во френелевской области, то есть с расстояний z порядка α²/λ. Именно поэтому дифракция волн на воде (λ порядка 1 м) или дифракция звука в воздухе (λ порядка 0,1 м) может наблюдаться практически всегда, дифракция света (λ порядка 10^-3-10^-4 м) требует выполнения особых условий (игольчатое отверстие, острый край бритвы и т.п.), а для дифракции рентгеновских лучей (λ порядка 10^-6-10^-8 м) используют кристаллические решётки.

Позднее было показано, что в равных условиях оба подхода (и Юнга, и Френеля) приводят к одинаковым результатам, однако при конкретных рассмотрениях одному из них может быть отдано методическое предпочтение. Следует подчеркнуть, что широкое развитие идущего от Юнга метода поперечной диффузии связано с освоением всё более коротковолновых электромагнитных диапазонов (с появлением мазеров, лазеров и т.п.) и необходимостью соответствующего «электродинамического обеспечения» (смотри Квазиоптика). Более того, этот метод оказался адекватным некоторым нелинейным дифракционным задачам типа самофокусировки и самоканалирования электромагнитных волн.

Явление дифракции имеет место и в микромире (смотри Дифракция частиц), поскольку объектам квантовой механики свойственно волновое поведение.

Лит.: Фок В. А. Проблемы дифракции и распространения электромагнитных волн. М., 1970; Боровиков В. А., Кинбер Б. Е. Геометрическая теория дифракции. М., 1978; Ваганов Р. Б., Каценеленбаум Б. З. Основы теории дифракции. М., 1982.