Гиперзвуковoе течение

ГИПЕРЗВУКОВОЕ ТЕЧЕНИЕ, предельный случай сверхзвукового течения, при котором скорость v газа во всей области течения или в её значительной части велика по сравнению со скоростью звука а в газе (v >> а), т. е. Маха число М = v/а >> 1. Существуют и другие критерии гиперзвукового течения, например 1/М²<< 1. Резкой границы между сверхзвуковым и гиперзвуковым течениями не существует, но считается, что гиперзвуковое течение для воздуха наступает уже при М≥5.

Т. к. скорость звука по порядку величины равна средней скорости хаотического (теплового) движения молекул, то при гиперзвуковом течении кинетическая энергия поступательного движения частиц газа намного превосходит внутреннюю тепловую энергию газа. Поэтому при переходе поступательной механической энергии газа в тепловую при торможении газа в головной ударной волне, которая всегда образуется перед телом при сверх и гиперзвуковом его обтекании, за ней в ударном слое (области между головной ударной волной и обтекаемым телом) возникают области с очень высокой температурой (десятки тысяч градусов), в которых протекают многие физико-химические процессы (возбуждение колебательных степеней свободы молекул, диссоциация, ионизация, излучение и др.). Для гиперзвукового течения характерны: взаимодействие сильных ударных волн с пограничным слоем у поверхности тела, вязкое взаимодействие внешнего невязкого потока с пограничным слоем, интенсивный конвективный и радиационный нагрев обтекаемого тела с появлением аэродинамической эрозии (плавление, испарение, шелушение и др.), унос массы с обтекаемой поверхности. При расчётах гиперзвукового течения учитываются как эффекты, которые возникают вследствие больших чисел Маха (газодинамические), так и эффекты, возникающие вследствие высокой температуры газа в ударном слое (физико-химические).

Теория гиперзвукового течения развивалась, начиная с 1950-х годов главным образом в связи с задачами аэродинамики и теплообмена при полётах межконтинентальных ракет, спутников, затем - космических зондов, а с 1970-х годов - планирующих космических аппаратов (КА) многократного использования («Буран», «Спейс Шаттл»). Все КА совершают полёт с гиперзвуковыми скоростями в верхних разреженных слоях атмосферы в режиме больших Кнудсена чисел: Кn = l/L >> 1 (l - средняя длина свободного пробега молекул в окружающей атмосфере, L - характерная макроскопическая длина тела). Первоначально теория гиперзвукового течения развивалась в рамках приближения идеального (невязкого) газа применительно к проблеме входа КА в плотные слои атмосферы Земли и планет. При очень больших числах М набегающего потока, когда 1/М²<< 1, параметры газа [ν/ν_∞, ρ/ρ_∞, р/(ρ_∞ν²_∞)] в ударном слое перестают зависеть от условий в набегающем потоке (ν, ρ, р - скорость, плотность и давление газа за ударной волной, v_∞ и ρ _∞ - скорость и плотность газа в набегающем потоке). Это свойство называют стабилизацией течения около тел при больших числах М.

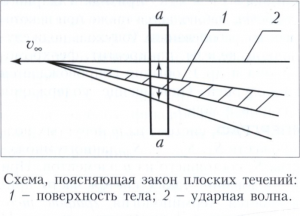
При гиперзвуковом обтекании тонких заострённых впереди тел вращения из теории следует так называемый закон плоских сечений, или принцип эквивалентности: частицы газа испытывают малое продольное смещение, но смещаются (выталкиваются) только перпендикулярно направлению движения тела от поверхности тела 1 к ударной волне 2 (рис.), оставаясь в исходной плоскости а-а, то есть движение частиц является плоским, тем самым реализуется эквивалентность установившегося трёхмерного гиперзвукового обтекания тонких заострённых тел с неустановившимися двумерными течениями.

На практике гиперзвуковые аппараты имеют слегка затупленные носок и передние кромки для уменьшения аэродинамического нагрева. Поэтому проблеме гиперзвукового обтекания затупленных тел уделяется особое внимание. Оценки показывают, что влияние малого затупления при гиперзвуковой скорости необходимо учитывать, даже когда размером затупленной части можно пренебречь. Если при движении тела в плоском слое соблюдается принцип эквивалентности, то в момент входа в этот слой переднего конца тела наличие малого затупления вызывает мгновенный сосредоточенный подвод энергии к газу - возникает задача о сосредоточенном взрыве. Эта взрывная аналогия позволила распространить закон подобия, установленный ранее для заострённых тонких тел, на тела с малым затуплением.

Давление на поверхности тела при очень больших значениях числа Маха в набегающем потоке М_∞ →∞ и γ → 1 (γ = c_p/c_V - отношение теплоёмкостей газа при постоянном давлении и постоянном объёме) может быть определено по формуле р = р_∞v_∞² sin²α, где α - угол между касательной к поверхности тела и направлением скорости набегающего потока. Было установлено, что если эту формулу дополнить коэффициентом, дающим правильное значение давления при α = π/2, то давление на наветренной стороне затупленных носовых частей определяется довольно точно. Эта теория получила название «модифицированной теории Ньютона», и, несмотря на её, по сути, эмпирическое происхождение, она оказалась очень полезной для определения давления, особенно на поверхностях сложной конфигурации.

При гиперзвуковых скоростях полёта пограничный слой утолщён из-за высокой температуры в нём, что приводит к возникновению взаимодействия между вязким течением в пограничном слое и внешним, по существу невязким, потоком. Давление, индуцированное взаимодействием вязкого и невязкого потоков, пропорционально М³_∞, откуда следует, что учёт вязкости необходим при расчётах характеристик гиперзвукового течения.

Для решения задач гиперзвукового обтекания тел используются различные модели в зависимости от значений Рейнольдса числа Re (уменьшающегося с увеличением высоты полёта). При больших значениях числа Re (Re > 10⁶) пользуются асимптотическими моделями идеальной жидкости в сочетании с теорией пограничного слоя (ламинарного или турбулентного), учитывая физико-химические процессы, происходящие в газе при высокой температуре. С уменьшением числа Re всё большую часть области течения между ударной волной и телом начинает занимать слой со значительным влиянием вязкости, так что необходимо учитывать обратное влияние пограничного слоя на внешний поток, а также влияние на пограничный слой поперечного градиента скорости (завихрённости) во внешнем потоке. При Re<10⁵ слой с влиянием вязкости занимает всю область между головной ударной волной и поверхностью тела. Для расчёта течения в этом слое применяют так называемую модель вязкого ударного слоя. При дальнейшем уменьшении числа Re (Re < 10³) уже нельзя пренебречь толщиной ударной волны по сравнению с толщиной слоя газа между ней и обтекаемым телом. Этому в условиях земной атмосферы соответствуют столь низкие значения плотности газа, что при них газодинамическая модель сплошной среды должна заменяться молекулярно-кинетической моделью.

Начиная с 1980-х годов гиперзвуковые течения интенсивно исследуются с помощью численных методов. Развитие эффективных численных методов и мощных ЭВМ позволило рассчитывать всё поле течения около трёхмерных аппаратов с учётом различных физико-химических процессов в ударном слое. Успешные полёты пилотируемых КА, а также возвращение на Землю космических зондов после исследования планет Солнечной системы - лучшее подтверждение высокого уровня теоретических и экспериментальных исследований гиперзвуковых течений.

Лит.: Черный Г. Г. Течение газа с большой сверхзвуковой скоростью. М., 1959; Хейз У .Д., Пробстин Р. Ф. Теория гиперзвуковых течений. М., 1962; Дорренс У. Х. Гиперзвуковые течения вязкого газа. М., 1966; Лунев В. В. Гиперзвуковая аэродинамика. М., 1975; Пилюгин Н. Н., Тирский Г. А. Динамика ионизированного излучающего газа. М., 1989; Park С. Nonequilibrium hypersonic aerothermodynamic. N. Y., 1990.