Гомологическая алгебра

ГОМОЛОГИЧЕСКАЯ АЛГЕБРА, раздел алгебры, основным объектом изучения которого являются производные функторы на различных категориях алгебраических объектов (смотри Категорий теория). В разных разделах математики часто возникают последовательности гомоморфизмов абелевых групп (или, более общо, модулей над кольцом)

в которых последовательное выполнение двух гомоморфизмов даёт нулевой гомоморфизм, то есть для всякого n образ im d_n+1 содержится в ядре ker d_n. Такие последовательности называются комплексами.

Примерами последовательностей С являются последовательности, в которых группы С_n порождаются простейшими геометрическими объектами (симплексами, клетками клеточного комплекса, сингулярными симплексами топологического пространства), а гомоморфизмы d_n задаются переходом к границам соответствующих объектов (смотри Топология), а также последовательности С, где С_n - пространства дифференциальных форм степени n, а отображения d_n задаются дифференцированием коэффициентов форм.

Гомоморфизмы d_n называют граничными отображениями, а также дифференциалами. Факторгруппы H_n(С) =  kerd_n/imd_n+1 называются группами гомологий комплекса С. Если все группы гомологий нулевые, H_n(С) = 0 (т.е. ker d_n = im d_n+1) для всех n, то последовательность С называется точной. Группы гомологий комплекса измеряют его отклонение от точной последовательности. Для конечного комплекса (когда С_n отличны от нуля лишь для конечного числа значений n) при переходе от групп С_n к группам гомологий H_n(С) сохраняется эйлерова характеристика χ(С) = Σ(-l)ⁿrankС_n, где rankC_n - ранг группы С_n. Простейшим, но нетривиальным частным случаем этого общего факта является теорема Эйлера, состоящая в том, что в трёхмерном пространстве число вершин выпуклого многогранника минус число его рёбер плюс число граней равно двум.

Понятие комплекса возникло в 1920-е годы как обобщение важных инвариантов топологических многообразий - чисел Бетти и коэффициентов кручения, введённых в конце 19 века в работах итальянского математика Э. Бетти и А. Пуанкаре и являющихся одним из первых источников идей гомологической алгебры. Другим источником методов гомологической алгебры явилась теория расширений групп (развитая в работах немецкого математика О. Шрайера в 1920-х годах). Она привела к построению групп гомологий для групп, ассоциативных алгебр, алгебр Ли и других алгебраических структур (в наиболее общем виде - гомологий алгебр над операдами). В основе их построения лежат специальные классы комплексов модулей. В алгебре одним из первых подобные конструкции стал систематически применять Д. Гильберт в конце 19 века. Пусть f₁ ,... , f_m - многочлены от n переменных. Идеал, порождённый ими, не будет свободным модулем, поскольку между этими многочленами существуют соотношения (сизигии, в терминологии Гильберта), то есть существуют векторы (а₁, а_m), компонентами которых являются многочлены, такие, что f₁а₁ + ... +f_ma_m=0. Множество Ω¹ таких соотношений также является модулем над кольцом многочленов и не обязательно свободным, так как между его порождающими снова имеются соотношения, образующие новый модуль Ω² и так далее. Теорема Гильберта утверждает, что через n шагов этот процесс прекратится, т. е. что Ω^n-1 - свободный модуль, и можно взять Ωⁿ = 0. Аналогичное утверждение верно, если считать f₁, ..., f_m элементами любого модуля над кольцом многочленов от n переменных, только последовательность оборвётся на (n + 1)-м шаге. На языке точных последовательностей эта теорема означает, что у произвольного модуля М над кольцом многочленов от n переменных имеется конечная свободная резольвента

т.е. точная последовательность свободных модулей F₁, F₂, ..., в которой модуль F_n+i можно выбрать нулевым.

О многих свойствах модулей и колец можно судить, зная только длины соответствующих резольвент. Так, проективная размерность модуля определяется как длина его наименьшей проективной резольвенты. Глобальной размерностью кольца R называется точная верхняя грань проективных размерностей R-модулей. Глобальная размерность равна нулю в точности для классических полупростых колец. Конечность глобальной размерности коммутативного кольца в применении к кольцам функций на алгебраических многообразиях позволяет характеризовать те многообразия, все точки которых неособы.

Во многих областях современной математики используется наглядный язык гомологической алгебры, важнейшим инструментом которого наряду с комплексами и точными последовательностями служат коммутативные диаграммы - ориентированные графы, в которых вершины обозначают рассматриваемые объекты, стрелки - их отображения, причём композиции отображений, соответствующих двум путям в графе с общим началом и концом, совпадают. Например, диаграмма

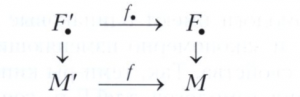
иллюстрирует тот факт, что любое отображение модулей f: M’→M  продолжается до морфизма их свободных резольвент f. : F.’ → F..

Переход от модулей к резольвентам является необходимым этапом общей операции перехода от какого-либо исходного функтора к его производному функтору. Теория производных функторов была развита в монографии А. Картана и французского математика С. Эйленберга «Homological Algebra» (1956). Частными случаями в общей теории производных функторов являются как упомянутые выше группы гомологий в топологии и в алгебре, так и многие конструкции, возникающие в комплексном анализе, алгебраической геометрии, теории представлений. Теория производных функторов позволила унифицировать подход к этим конструкциям и привела к созданию современного аппарата производных категорий.

Гомологическая алгебра имеет многочисленные применения в таких областях математики, как алгебраическая теория чисел, алгебраическая и дифференциальная геометрия, топология, теория функций многих комплексных переменных, теория дифференциальных уравнений в частных производных, функциональный анализ, а также в теоретической физике.

Лит.: Картан А., Эйленберг С. Гомологическая алгебра. М., 1960; Гротендик А. О некоторых вопросах гомологической алгебры. М., 1961; Маклейн С. Гомология. М., 1966; Браун К. С. Когомологии групп. М., 1987; Гельфанд С. И., Манин Ю. И. Методы гомологической алгебры. М., 1988. Т. 1; Кузьмин Ю. В. Гомологическая теория групп. М., 2006.