Индексы в статистике

ИНДЕКСЫ в статистике (от латинского index - указатель, показатель), показатели относительного изменения данного уровня исследуемого явления по сравнению с другим его уровнем, принятым за базу сравнения. В качестве такой базы может быть использован уровень за какой-либо прошлый период времени (динамические индексы) или уровень того же явления на другой территории (территориальные индексы).

Простейший показатель, используемый в индексном анализе, - индивидуальный индекс, характеризующий изменение во времени экономических величин, относящихся к одному объекту. Так, индивидуальный индекс  цены рассчитывается следующим образом:

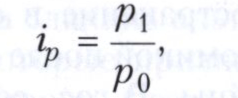
где р₁ - цена товара в текущем периоде; Р₀ - цена товара в базисном (предшествующем) периоде.

Данный индекс  показывает, как выросла или снизилась цена товара в текущем периоде по сравнению с базисным периодом.

Изменение физической массы проданного товара в натуральном выражении измеряется индивидуальным индексом физического объёма реализации:

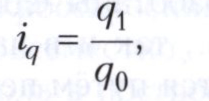
где q₁ - количество товара в текущем периоде; q₀ - количество товара в базисном (предшествующем) периоде.

Изменение стоимостного объёма товарооборота по данному товару отражается в значении индивидуального индекса товарооборота. Для его расчёта товарооборот текущего периода (произведение цены на количество проданного товара) сравнивается с товарооборотом предшествующего периода:

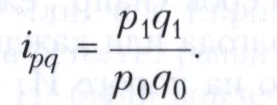
Данный индекс  также может быть получен как произведение индивидуального индекса цены и индивидуального индекса физического объёма реализации.

В отличие от индивидуальных индексов, сводные индексы позволяют обобщить показатели по нескольким видам товаров, нескольким видам продукции, по ценным бумагам нескольких эмитентов и т. д. Исходной формой сводного индекса является агрегатная форма. Сводные индексы также могут исчисляться в среднеарифметической и среднегармонической формах.

Сводный индекс  товарооборота в агрегатной форме показывает изменение стоимостного объёма товарооборота по товарной группе. При этом определяется совокупный объём товарооборота по n товарам в текущем периоде:

Аналогично определяют совокупный объём товарооборота для базисного периода:

Сводный индекс  товарооборота получают как отношение данных агрегатов:

Величина индекса товарооборота формируется под воздействием двух факторов - на неё оказывают влияние как изменение цен на товары, так и изменение объёмов их реализации. Для того, чтобы оценить изменение только цен (индексируемой величины), количество проданных товаров (веса индексы) фиксируют на каком-либо постоянном уровне. Таким способом получают сводные индексы цен (смотри Индексы цен).

Сводный индекс  физического объёма реализации характеризует изменение количества проданных товаров по той или иной товарной группе; при этом входящие в группу товары могут быть непосредственно несоизмеримы, существенно отличаться по своим характеристикам, в том числе и по единицам измерения (предположим, часть товаров измеряется в кг, часть - в штуках, часть - в литрах). Весами в данном случае выступают цены, которые фиксируются на уровне базисного или текущего периода, например:

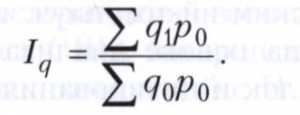
Знаменатель данного индекса отражает фактический стоимостной объём товарооборота в базисном периоде. Числитель же - условная величина, показывающая, каким бы был стоимостной объём товарооборота в текущем периоде при условии сохранения цен на уровне базисного периода. В итоге данный индекс  отражает изменение физического объёма реализации по группе товаров, объёмы которых непосредственно в натуральном выражении суммировать нельзя.

Между индексами товарооборота, цен и физического объёма реализации существует следующая взаимосвязь:

Аналогично приведённым выше индексам рассчитываются и другие сводные индексы в агрегатной форме (себестоимости, урожайности и пр.).

Индексы  позволяют получать сводную оценку изменения наблюдаемых показателей постоянно - месяц за месяцем, год за годом. При этом для достижения сопоставимости они рассчитываются по единой методологии. Такая методология, или схема расчёта индекса за n последовательных временных периодов, называется системой индексов.

В зависимости от информационной базы и целей исследования индексная система может включать индексы цепные или базисные, с переменными или постоянными весами. Например, при расчёте индекса цен, если сравнивать цены каждого периода с ценами периода предшествующего, получаемая индексная система будет включать цепные индексы, отражающие изменение цен за каждый из периодов рассматриваемого временного интервала. При этом в качестве весов используют объёмы реализации каждого конкретного периода или же постоянные объёмы какого-либо периода, принятого в качестве базисного. В первом случае индексная система включает цепные индексы с переменными весами:

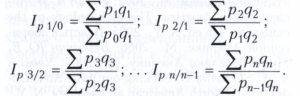
При использовании весов базисного периода получают цепные индексы цен с постоянными весами:

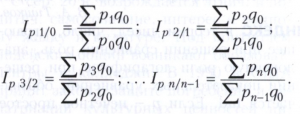
Использование постоянных весов более предпочтительно, поскольку рассчитываемые таким образом индексы мультипликативны, т. е. их можно последовательно перемножать и получать величину показателя за более продолжительный период. Так, например, располагая индексы цен за 3 последовательных месяца, можно получить сводную оценку изменения цены в целом за квартал и т.п. Индексы с переменными весами такой возможности не предоставляют.

При сравнении цен каждого периода с ценами какого-либо базисного периода (как правило, начального) получаемая индексная система включает базисные индексы, отражающие изменение цен накопленным итогом, то есть с начала рассматриваемого временного интервала (например, изменение цен в январе по сравнению с декабрём предшествующего года, в феврале - по сравнению с тем же декабрём и т.д.). При этом в качестве весов также можно использовать объёмы реализации каждого конкретного периода или же постоянные объёмы периода, принятого за базисный. Система базисных индексов с переменными весами имеет следующий вид:

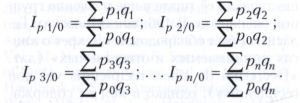
Базисные индексы цен с постоянными весами рассчитываются по формулам:

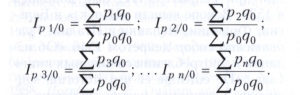
При расчёте индексов используют не только агрегатную, но и средние их формы - среднеарифметическую и среднегармоническую, т.к. любой сводный индекс  можно представить как среднюю взвешенную из индексов индивидуальных. Использование средних форм связано с тем, что часть необходимой для расчёта индекса информации в ряде случаев отсутствует или данные базируются на результатах выборочных обследований, которые приобретают всё большее значение в статистической практике. Например, при расчёте сводного индекса цен по методу Пааше используют следующую замену:

Тогда сводный индекс цен будет выражен в форме средней гармонической:

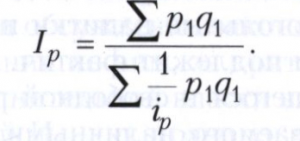
Данный сводный индекс цен в среднегармонической форме соответствует сводному индексу Пааше в агрегатной форме. Для получения среднего индекса цен, соответствующего индексу Ласпейреса, в формуле последнего используется следующая замена:

С учётом этой замены сводный индекс цен в среднеарифметической форме имеет вид:

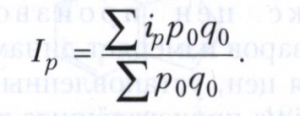
Среднеарифметическая и среднегармоническая формы также используются при расчёте сводного индекса физического объёма товарооборота и других индексов.

Индексы  используются не только для оценки динамики показателей, характеризующих разнородные в качественном отношении совокупности (товарные группы). Даже если рассматриваемая совокупность однородна (товар одного вида), на величине результативного показателя - средней цены данного товара - отражается влияние структурных изменений, например изменений в структуре его реализации по территориям. В этом случае в индексном анализе используются индексы переменного и фиксированного состава, а также индексы структурных сдвигов.

Индекс   цен переменного состава представляет собой соотношение средних значений цены данного товара за 2 рассматриваемых периода:

Значение индекса отражает изменение средней цены как за счёт изменения региональных уровней цен, так и за счёт изменений в структуре реализации товара по регионам. Воздействие структурного фактора оценивают на основе индекса структурных сдвигов, зафиксировав цены на уровне базисного периода:

Индекс цен фиксированного состава не учитывает структурные сдвиги, а характеризует изменение средней цены товара, обусловленное лишь изменением региональных цен:

Взаимодействие учитываемых в данных И. факторов отражается следующей взаимосвязью:

В отличие от представленных выше динамических индексов, территориальные индексы служат для сравнения показателей в пространстве, то есть по городам, районам, областям и т. п. Важную роль играют территориальные индексы цен, являющиеся незаменимым инструментом исследования в практике международных сравнений уровней цен, в том числе между странами СНГ.

Построение территориальных индексов имеет определённые особенности, связанные с выбором базы сравнения и весов, или уровня, на котором фиксируются веса. Один из вариантов расчёта территориальных индексов цен заключается в том, что в качестве весов принимаются объёмы проданных товаров i-го вида (i = 1,2,..., n) по двум территориям, вместе взятым:

где q_ia - количество i-го товара, проданного на территории А; q_ib - количество i-го товара, проданного на территории В.

Территориальный индекс цен в этом случае рассчитывается по формуле:

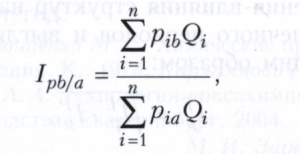
где p_ib - цена i-го товара на территории В; р_ia - цена i-го товара на территории А.

При расчёте территориальных индексов данным способом в их формуле вместо суммарных весов могут использоваться некоторые теоретические или стандартизованные веса; в качестве таких весов также может выступать структура продажи данных товаров по более крупному территориальному образованию.

Лит.: Гусаров В. М. Теория статистики. М., 1998; Статистика. Курс лекций. М., 1998; Общая теория статистики. 5-е изд. М., 2007; Теория статистики. 4-е изд. М., 2007.

В. Г. Минашкин.