Интегральное исчисление

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ, раздел математического анализа, в котором изучаются интегралы, их свойства, методы вычисления и различные приложения. Интегральное исчисление тесно связано с дифференциальным исчислением и составляет вместе с ним основную часть математического анализа (или анализа бесконечно малых). Центральными понятиями интегрального исчисления являются понятия определённого и неопределённого интегралов функций одной действительной переменной.

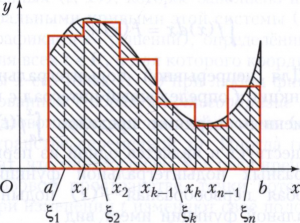
Определённый интеграл. К этому понятию приводят две фундаментальные задачи: задача о вычислении пути, пройденного движущейся вдоль оси Оу материальной точкой за промежуток времени от х = а до х = b, а<b, по известной в любой момент времени х скорости f(х) этой точки, и геометрическая задача о вычислении площади так называемой криволинейной трапеции, то есть фигуры, ограниченной графиком функции у = f(х) на отрезке а ≤ х ≤ b, осью абсцисс и двумя вертикальными прямыми х = а и х = b (на рисунке эта фигура заштрихована).

Для решения первой задачи промежуток времени а ≤ х ≤ b можно разбить на малые промежутки, ограниченные моментами времени а = х₀<х₁<х₂<...<х_n-1<х_n = b. На каждом малом промежутке времени x_k-1 ≤ х ≤ x_k скорость меняется мало и её можно считать постоянной и равной f(ξ_k), где ξ_k - некоторое значение времени из промежутка [x_k-1, x_k], k = 1…n. При этом путь S[x_k-1, x_k], пройденный движущейся точкой за промежуток времени от x_k-1 до x_k, приближённо можно считать равным произведению f(ξ_k) на длину Δx_k = x_k -x_k-1, промежутка [x_k-1, x_k], т.е. S[x_k-1, x_k] = f(ξ_k)Δx_k. В таком случае путь S[а, b], пройденный движущейся точкой за весь промежуток времени от х = а до х= b, приближённо равен сумме

Точное значение пути S[а, b] получается, если в сумме (1) перейти к пределу при стремлении к нулю наибольшей из длин Δx_k (при этом общее число n частичных промежутков будет неограниченно возрастать). Т.е. если d - наибольшая из длин Δx_k, то

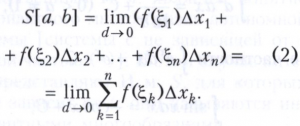
Суммы (1) можно рассматривать для произвольной функции f(х), заданной на отрезке а ≤ х ≤ b, их называют интегральными суммами, отвечающими данным разбиениям отрезка [а, b], а предел, стоящий в правой части (2), - определённым интегралом от функции f по отрезку [а, b]. Для широкого класса функций f(х) этот предел существует и не зависит ни от выбора конкретных разбиений х₀<х₁ < ... <х_n, ни от выбора точек ξ_k, x_k-1 ≤ ξ_k ≤x_k, k=1,..,n. В этом случае говорят, что определённый интеграл от функции f(х) по отрезку [а, b] существует, его обозначают ∫_a^b f(х)dx. В этом обозначении символ ∫ (удлинённое S - первая буква слова Summa) называется знаком интеграла, f(х) - подынтегральной функцией, а числа а и b - соответственно нижним и верхним пределами интегрирования.

Решение второй задачи (о вычислении площади заштрихованной на рисунке криволинейной трапеции) основано на том, что интегральная сумма (1) геометрически представляет собой сумму площадей прямоугольников, основаниями которых служат отрезки [x_k-1, x_k ] длины Δx_k, а высотами - отрезки длины f(ξ_k), то есть сумма (1) равна площади ступенчатой фигуры, обведённой на рисунке красной линией, а предел, стоящий в правой части (2), то есть интеграл ∫_a^b f(х)dx равен площади этой криволинейной трапеции.

Определённый интеграл обладает свойством линейности: из существования определённых интегралов от функций f₁(х) и f₂(х) по отрезку [а, b] вытекает, что для любых действительных чисел α и ß

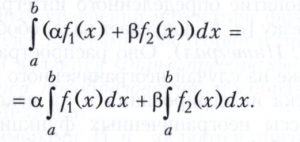
Кроме того, при а ≥ b по определению полагают

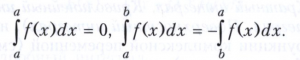
Значение определённого интеграла не зависит от обозначения переменной интегрирования, т. е.

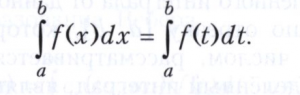
К вычислению определённых интегралов, кроме указанных выше двух задач, приводят также задачи о вычислении площадей, ограниченных кривыми, длин дуг гладких кривых, площадей поверхностей тел, объёмов тел, а также задачи определения координат центров тяжести, моментов инерции и другие задачи естествознания и техники. Например, длина дуги плоской гладкой кривой, заданной на отрезке а ≤ х ≤ b уравнением у = f(х), выражается интегралом

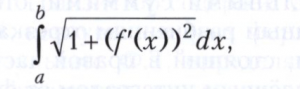
объём тела, образованного вращением этой дуги вокруг оси Ох, - интегралом

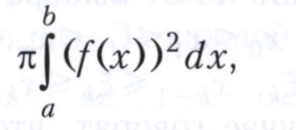
а площадь поверхности этого тела - интегралом

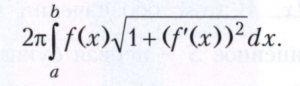
Существуют различные способы интегрирования, то есть вычисления определённых интегралов. В отдельных случаях удаётся непосредственно вычислить предел, стоящий в правой части (2). Некоторые определённые интегралы удаётся вычислить с помощью неопределённых интегралов (смотри ниже). Однако, как правило, приходится прибегать к приближённому вычислению определённых интегралов, применяя различные квадратурные формулы.

В случае, когда подынтегральная функция f, кроме переменной х, по которой идёт интегрирование, зависит ещё от переменной а, рассматривают определённые интегралы вида

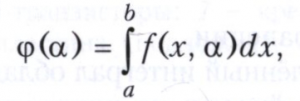
называемые интегралами, зависящими от параметра. Они служат основным средством для изучения многих специальных функций.

Понятие определённого интеграла по отрезку [а, b] допускает различные обобщения (смотри Интеграл). Оно распространяется также на случай неограниченного промежутка интегрирования и на некоторые классы неограниченных функций (такие обобщения называют несобственными интегралами), а также на функции многих действительных переменных (смотри Кратный интеграл, Криволинейный интеграл, Поверхностный интеграл), на функции комплексной переменной (смотри Коши интеграл) и на вектор-функции (смотри Остроградского формула, Стокса формула).

Неопределённый интеграл. Помимо определённого интеграла от данной функции f по отрезку [а, b], который является числом, рассматривается также неопределённый интеграл, являющийся функцией, получающейся из f с помощью операции интегрирования, которая обратна операции дифференцирования. К неопределённому интегралу приводит, например, задача о нахождении функции, выражающей путь, пройденный движущейся точкой, по скорости этой точки. При дифференцировании данной функции ищется её производная. При интегрировании функции ищется функция, называемая первообразной или примитивной, производная которой равна данной функции. Функция F(х) является первообразной функции f(х) на интервале а < х < b, если всюду на этом интервале функция F(х) имеет производную, удовлетворяющую равенству F’(х) = f(х), или, что то же самое, если всюду на этом интервале dF(х) = f(х)dx. Если функция F(х) является первообразной функции f(х) на данном интервале, то и функция F(х) + С, где С - любая постоянная, также является первообразной функции f(х) на этом интервале (поскольку производная постоянной равна нулю). Любые две первообразные функции для f(х) отличаются лишь постоянным слагаемым. Если F(х) является одной из первообразных функции f(х), то все первообразные функции f(х) имеют вид F(х) + С; это выражение называется неопределённым интегралом от функции f(x) и обозначается ∫ f(х)dx, таким образом,

Для непрерывной подынтегральной функции f определённый интеграл с переменным верхним пределом  ∫_а^х f(t)dt существует и является одной из первообразных подынтегральной функции. Любая первообразная F(х) подынтегральной функции имеет вид

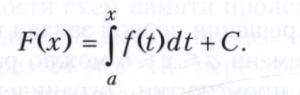
Следствием этого равенства является так называемая основная формула интегрального исчисления (формула Ньютона - Лейбница)

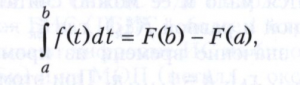
выражающая определённый интеграл через разность значений любой первообразной на концах интервала интегрирования.

Взаимно обратный характер операций интегрирования и дифференцирования выражается равенствами

из которых вытекает возможность получения из формул дифференцирования соответствующих формул интегрирования:

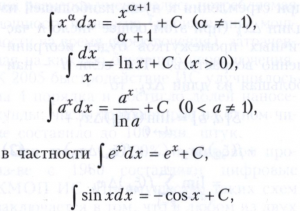
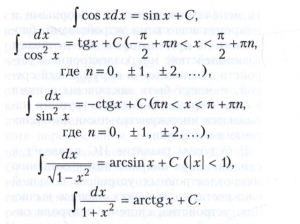
Неопределённый интеграл обладает справедливым с точностью до произвольного постоянного слагаемого линейным свойством

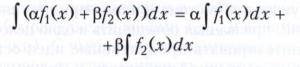
(α и β- произвольные действительные числа).

В то время как производные всех элементарных функций выражаются через элементарные функции, интегралы от элементарных функций не всегда выражаются через элементарные функции, то есть, как говорят, не всегда «берутся в конечном виде». Интегральное исчисление располагает лишь отдельными приёмами интегрирования в конечном виде. Среди правил интегрирования основными являются правило интегрирования по частям, опирающееся на равенство

и интегрирование заменой переменной, опирающееся на то, что, если

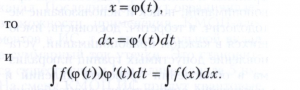
К классу функций, интегралы от которых всегда выражаются через элементарные функции, относятся множество всех рациональных функций (т. е. отношений двух многочленов Р(х) и Q(х)), множество функций, рационально зависящих от √(ах² +bх + с) и от х или от х и от рациональной степени дроби (ax + b)/(cx + d), множество функций, рационально зависящих от cos x и sin x.

Функции, которые представляются неопределёнными интегралами, не берущимися в конечном виде, представляют собой новые трансцендентные функции, некоторые из которых хорошо изучены (смотри, например, Интегральный логарифм, Интегральные синус и косинус, Интегральная показательная функция).

О расширении и обобщении понятия интеграла смотри Интеграл.

Историческая справка. Возникновение интегрального исчисления связано с нахождением площадей и объёмов. Ряд задач такого рода был решён математиками Древней Греции. Античная математика предвосхитила идеи интегрального исчисления в значительно большей степени, чем дифференциального исчисления. Большую роль при решении таких задач играл исчерпывания метод, созданный Евдоксом Книдским и широко применявшийся Архимедом. Однако Архимед не выделил общего содержания интеграционных приёмов и понятия об интеграле, и тем более не создал алгоритма интегрального исчисления. Учёные Среднего и Ближнего Востока в 9-15 веках изучали и переводили труды Архимеда на общедоступный в их среде арабский язык, но существенно новых результатов в интегральном исчислении они не получили. Деятельность европейских учёных в это время была ещё более скромной. Лишь в 16-17 веках развитие естественных наук поставило перед математиками Европы ряд новых задач, в частности задачи нахождения квадратур, кубатур и определение центров тяжести. Труды Архимеда, впервые изданные в 1544 году (на латинском и греческом языках), стали привлекать широкое внимание, и их изучение явилось одним из важнейших отправных пунктов дальнейшего развития интегрального исчисления. Античный «неделимых» метод был возрождён И. Кеплером. В более общей форме идеи этого метода были развиты Б. Кавальеры, Э. Торричелли, Дж. Валлисом, Б. Паскалем. Методом «неделимых» был решён ряд геометрических и механических задач. К этому же времени относятся опубликованные позднее работы П. Ферма по квадрированию парабол n-й степени, а затем - работы Х. Гюйгенса по спрямлению кривых.

В итоге этих исследований выявилась общность приёмов интегрирования при решении внешне несходных задач геометрии и механики, приводившихся к квадратурам как к геометрическому эквиваленту определённого интеграла. Заключительным звеном в цепи открытий этого периода было установление взаимно обратной связи между задачами на проведение касательной и на квадратуры, то есть между дифференцированием и интегрированием. Основные понятия и алгоритм интегрального исчисления были созданы независимо друг от друга И. Ньютоном и Г. В. Лейбницем. Последнему принадлежит термин «интегральное исчисление» и обозначение интеграла ∫ydx.

При этом в работах Ньютона основную роль играло понятие неопределённого интеграла (флюенты; смотри Флюксий исчисление), тогда как Лейбниц исходил из понятия определённого интеграла. Дальнейшее развитие интегрального исчисления в 18 веке связано с именами И. Бернулли и особенно Л. Эйлера. В начале 19 века интегральное исчисление вместе с дифференциальным исчислением было перестроено О. Коши на основе теории пределов. В развитии интегрального исчисления в 19 веке приняли участие М. В. Остроградский, В. Я. Буняковский, П. Л. Чебышев. В конце 19 - начале 20 века развитие теории множеств и теории функций действительной переменной привело к углублению и обобщению основных понятий интегрального исчисления (Б. Риман, А.Лебег и др.).

Лит.: История математики с древнейших времен до начала XIX столетия: В 3 т. М., 1970-1972; Рыбников К. А. История математики. М., 1994; Никольский С. М. Курс математического анализа. 6-е изд. М., 2001; Зорич В. А. Математический анализ. 4-е изд. М., 2002. Ч. 1-2; Кудрявцев Л. Д. Курс математического анализа: В 3 т. 5-е изд. М., 2003-2006; Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. 8-е изд. М., 2003-2005. Т. 1,3; Ильин В. А., Куркина А. В. Высшая математика. 2-е изд. М., 2004; Ильин В. А., Позняк Э. Г. Основы математического анализа. М., 2005. Ч. 1. 7-е изд. М., 2006. Ч. 2. 5-е изд.; Ильин В. А., Садовничий В. А., Сендов Бл. Х. Математический анализ. 3-е изд. М., 2006. Ч. 1-2.

В. А. Ильин.