Канал связи (в теории информации)

КАНАЛ СВЯЗИ в теории информации, математическая модель устройства, предназначенного для передачи информации. Информации теория отвлекается от конкретной природы таких устройств, подобно тому, как геометрия изучает геометрические фигуры и тела, отвлекаясь от материала, из которого они изготовлены. Различные конкретные системы связи рассматриваются только с точки зрения количества информации, которое может быть надёжно передано с их помощью. В теории информации канал связи задаётся множеством {х} допустимых сообщений (сигналов) на входе, множеством {у} сообщений (сигналов) на выходе и набором условных вероятностей р(у|х) получения сигнала у на выходе при входном сигнале х. Эти условные вероятности описывают статистические свойства шумов (помех), искажающих сигналы в процессе передачи. В случае когда р(у|х) = 1 при у = х для всех х ∈ {х}, канал связи называется каналом без шумов. В соответствии со структурой входных и выходных сигналов выделяют дискретные и непрерывные каналы связи. В дискретных каналах связи сигналы на входе и на выходе представляют собой последовательности букв из одного и того же или различных алфавитов (смотри Код). В непрерывных каналах связи входной и выходной сигналы суть функции непрерывного параметра, который обычно является временем. Возможны также смешанные случаи, но обычно предпочитают рассматривать один из двух указанных случаев.

Способность канала связи передавать информацию характеризуется некоторым числом - пропускной способностью (ёмкостью) канала, которая определяется как максимальное количество информации относительно сигнала на входе, содержащееся в сигнале на выходе (в расчёте на единицу времени). Точнее, пусть входной сигнал Х принимает значения х ∈ {х} с вероятностями р(х). Тогда по формулам теории вероятностей можно рассчитать как вероятности q(у) того, что сигнал Y на выходе примет значение у, q(y)  =∑_хр(х)р(у|х), так и вероятности р(х, у) совмещения событий Х = х, Y = у, р(х, у) = р(х)р(у|х). По этим величинам вычисляется количество информации

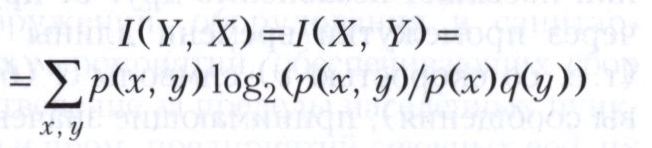
и его среднее значение на единицу времени

где Т - длительность передачи сигнала Х. Верхняя граница С величин R, взятая по всем источникам сообщений на входе, называется пропускной способностью канала связи. Вычисление пропускной способности, подобно вычислению энтропии, легче в дискретном случае и сложнее в непрерывном, где оно основывается на теории стационарных случайных процессов.

В теории информации устанавливается, что в случае дискретного канала связи без шумов общее определение пропускной способности С равносильно следующему:

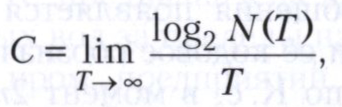
где N(Т) - число допустимых сигналов длительности  Т.

Пример 1. Пусть входной алфавит канала связи без шумов состоит из символов (букв) 0 и 1, передача каждого из которых занимает τ секунд. Допустимые сигналы длительностью Т=nτ представляются последовательностями длины n символов 0 и 1. Их число Ν(Τ) = 2ⁿ. В этом случае

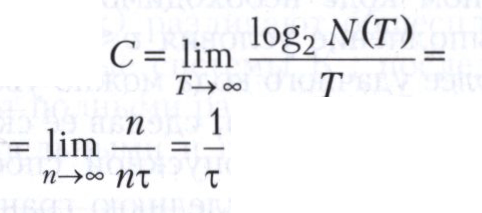
(двоичные ед./с).

Пример 2. Пусть символы 0 и 1 передаются за τ и 2τ с соответственно. Здесь допустимых сигналов длительностью Т = nτ будет меньше, чем в примере 1. Так, при n = 3 их будет всего 3 (вместо 8). Можно подсчитать, что

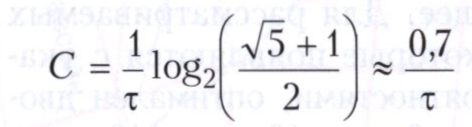
(двоичные ед./с).

При необходимости передачи сообщений по данному каналу связи приходится преобразовывать эти сообщения в допустимые сигналы канала связи, т. е. производить надлежащее кодирование. После передачи необходимо произвести операцию декодирования, т. е. операцию обратного преобразования сигналов в сообщения. Кодирование целесообразно производить так, чтобы среднее время, затрачиваемое на передачу, было возможно меньше. При одинаковой длительности передачи символов на входе канала связи это означает, что для кодирования сообщений надо выбирать наиболее экономный код с алфавитом, совпадающим со входным алфавитом каналом связи. При процедуре согласования источника с каналом связи возникает специфическое явление задержки (запаздывания), которое может пояснить следующий пример.

Пример 3. Пусть источник сообщений посылает независимо друг от друга через промежутки времени длины 1/υ (т. е. со скоростью υ) символы х (буквы сообщения), принимающие значения х₁, х₂, х₃, х₄ с вероятностями, равными соответственно 1/2, 1/4, 1/8, 1/8. Пусть канал связи без шумов такой же, как в примере 1, и кодирование осуществляется мгновенно. Полученный сигнал или передаётся по каналу связи, если последний свободен, или ожидает (помещается в память) до тех пор, пока канал связи не освободится. Если выбран, например, код х₁ =00, х₂=01, х₃=10, х₄=11 и υ≤τ/2 (т.е. 1/υ≥2τ), то за время между появлением двух последовательных значений х кодовое обозначение первого из них успевает передаться и канал связи освобождается. Таким образом, здесь между появлением какой-либо буквы сообщения и передачей её кодового обозначения по каналу связи проходит промежуток времени 2τ. Если υ > τ/2, то n-я буква сообщения появляется в момент (n - 1)/υ и её кодовое обозначение будет передано по каналу связи в момент 2nτ. Промежуток времени между появлением n-й буквы сообщения и моментом её получения после декодирования переданного сигнала будет больше, чем n(2τ-1/υ), эта величина стремится к бесконечности при n → ∞ т. е. в этом случае передача будет вестись с неограниченным запаздыванием. Поэтому для возможности передачи без неограниченного запаздывания при данном коде необходимо и достаточно выполнение условия υ≤τ/2. Выбором более удачного кода можно увеличить скорость передачи, сделав её сколь угодно близкой к пропускной способности канала связи, но эту последнюю границу невозможно превзойти (сохраняя требование ограниченности запаздывания). Сформулированное утверждение имеет общий характер и называется основной теоремой о канале связи без шумов.

В отношении примера 3 можно добавить следующее. Для рассматриваемых сообщений, которые появляются с указанными вероятностями, оптимален двоичный код х₁=0, х₂=10, х₃=110, х₄ = 111. Из-за различной длины кодированных сообщений время запаздывания для n-й буквы первоначального сообщения будет случайной величиной. При υ < 1/τ (1/τ -пропускная способность канал связи) и n → ∞ его среднее значение приближается к некоторому пределу m(υ), зависящему от υ. С приближением υ к критическому значению l/τ значение m(υ) растёт пропорционально (τ^-1 - υ)^-1. Это отражает общее положение: при приближении скорости передачи к максимальной возрастают время запаздывания и необходимый объём памяти кодирующего устройства.

Утверждение основной теоремы (с заменой безошибочной передачи на почти безошибочную) справедливо и для канала связи с шумами. Этот факт, по существу основной для всей теории передачи информации, называется теоремой Шеннона. Возможность уменьшения вероятности ошибочной передачи через канал связи с шумами достигается применением, так называемых помехоустойчивых кодов.

Пример 4. Пусть входной алфавит канала связи состоит из двух символов 0 и 1 и действие шумов сводится к тому, что каждый из этих символов при передаче может с небольшой вероятностью р перейти в другой или с вероятностью q =  1 - р остаться неискажённым. Применение помехоустойчивого кода сводится, по сути дела, к выбору нового алфавита на входе канала связи. Его буквами являются n-членные цепочки символов 0 и 1, отличающиеся одна от другой достаточным числом d знаков. Так, при n = 5 и d = 3 новыми буквами могут быть 00000, 01110, 10101, 11011. Поскольку при малых р вероятность более чем одной ошибки на группу из пяти знаков мала, то, даже искажённые, эти буквы почти не перепутываются. Например, если получен сигнал 10001, то он, скорее всего, возник из 10101. Оказывается, что при надлежащем выборе достаточно больших n и d такой способ значительно эффективнее простого повторения (т. е. использования алфавитов типа 000, 111). Однако возможное на этом пути улучшение качества передачи сопряжено с возрастающей сложностью кодирующих и декодирующих устройств. Например, если первоначально р = 10^-2 и требуется уменьшить это значение до р₁ = 10^-4, то следует выбирать длину n кодовой цепочки не менее 25 (или 380) в зависимости от того, желают ли использовать пропускную способность канала связи на 53% (или на 80%).

В конце 20 века в связи с развитием квантовой теории информации и квантовых компьютеров появились и исследуются квантовые каналы связи.

Лит. смотри при ст. Информация.

Ю. В. Прохоров.