Автоморфная Функция

АВТОМОРФНАЯ ФУНКЦИЯ - мероморфная функция, значения которой не изменяются, если её аргумент подвергается некоторым комплексно-аналитическим преобразованиям. К автоморфной функции относятся периодические функции и, в частности, эллиптические функции. Так, например, если указанные преобразования имеют вид z’ = z + ω, где ω - комплексное число, отличное от нуля, то получаются автоморфные функции, удовлетворяющие равенству f(z + ω) = f(z),  т. е. периодические функции с периодом ω. В этом примере преобразованием, не изменяющим функции, является сдвиг комплексной плоскости на вектор ω. Тот же сдвиг, повторенный сколько угодно раз, также не изменяет функции. В результате получается группа линейных преобразований z’ = z + nω, n = 0, ±1, ±2,..., не изменяющих f(z).

Автоморфные функции (и, более общо, автоморфные формы) изучаются в теории автоморфной функции, представляющей самостоятельный раздел математики. Обычно в теории автоморфных функций рассматриваются области D в комплексном пространстве Cⁿ и дискретные группы Г аналитических преобразований D в себя. Автоморфной формой f веса m на D называется аналитическая (или только мероморфная) функция, которая преобразуется под действием группы Г согласно соотношению

где f(γ) - якобиан отображения γ (z), а m - целое неотрицательное число. Если m = 0, то f является автоморфной функцией.

Факторпространство Х = D/Г, которое получается заменой элементов множества D на классы эквивалентности, порождённые группой Г, обладает комплексно-аналитической структурой (т. е. известно, какие функции на нём являются аналитическими, ими будут автоморфные функции). Если дано комплексно-аналитическое многообразие Х, то нахождение области D и дискретной группы Г таких, что Х = D/Г называется задачей униформизации многообразия Х. Если же даны область D и группа Г, то встаёт вопрос об описании пространства Х и прежде всего поля К автоморфной функции (или кольца автоморфных форм).

Примеры.

1. Пусть область D совпадает со всем пространством Cⁿ а Г = Z²ⁿ - группа параллельных переносов на векторы, принадлежащие дискретной группе в Cⁿ максимально возможного ранга 2n. Тогда пространство D/Г компактно, гомеоморфно тору и поле автоморфной функции К на Х имеет степень трансцендентности, не превосходящую n. Если выполнены дополнительные условия на группу Г (условия Римана - Фробениуса), то поле К содержит n алгебраически независимых функций и Х является проективным алгебраическим многообразием, или абелевым многообразием (смотри Алгебраическая геометрия). Для n = 1 эти условия выполняются всегда, автоморфные функции суть эллиптической функции и Х является эллиптической кривой.

2. Пусть D является верхней полуплоскостью в С. Группа G матриц второго порядка с действительными элементами и определителем, равным 1, действует на D дробно-линейными преобразованиями

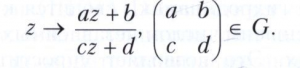
Пусть Г - дискретная подгруппа в G. Мероморфная функция f на D будет автоморфной формой веса m (m - целое неотрицательное число), если

Пусть факторпространство Х = D/Г компактно. Тогда Х является проективной неособой алгебраической кривой. С другой стороны, каждая такая кривая Х представима как факторпространство Х = D/Г (задача униформизации). Размерность пространства голоморфных автоморфных форм данного веса можно вычислить, используя теорему Римана - Роха на факторпространстве Х. Так, если группа Г не имеет неподвижных точек, то размерность равна (2m- 1 )(g- 1), если m> 1, равна g, если m= 1, и равна 1, если m = 0 (здесь g - род кривой Х).

3. Пусть D - снова верхняя полуплоскость, но Г - группа матриц второго порядка с целыми элементами. Автоморфные формы для группы Г определяются так же, как и в предыдущем примере, и называются в этой ситуации модулярными формами, а сама группа - модулярной группой. Факторпространство будет теперь некомпактным, но его можно дополнить конечным множеством точек так, что получится проективная алгебраическая кривая (такие кривые называются модулярными).

Теория автоморфных функций одного комплексного переменного была создана в конце 19 - начале 20 века в работах Ф. Клейна, А. Пуанкаре, Р. Кебе и др., в которых была решена задача униформизации для одномерных комплексных многообразий (римановых поверхностей). Был также описан класс дискретных групп, действующих в единичном круге на комплексной плоскости (или на всей комплексной плоскости), для которых поле К является полем алгебраических функций от одной переменной. Нетривиальные автоморфные функции строятся как отношения автоморфных форм одного и того же веса. Для построения последних Пуанкаре предложил конструкцию, получившую название рядов Пуанкаре.

Пусть h(z), zЄD, - произвольная голоморфная на D функция. Рядом Пуанкаре называется ряд

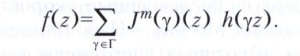
Если он сходится, то его сумма является автоморфной формой. Иногда группа Г содержит такую бесконечную подгруппу Г₀, что J(γ)(z) = 1 для γ Є Г₀. Тогда в определении ряда Пуанкаре нужно брать сумму по γ е Г/Г₀. Это имеет место для модулярной группы примера 3, где Г₀ отвечает дробно-линейным преобразованиям вида z→z + n, nЄZ. Эта конструкция даёт возможность строить автоморфные формы достаточно большого веса.

Приведённые выше примеры дискретных групп изучались в 19 веке, и дальнейшее развитие теории автоморфных функций шло по пути обобщения основных результатов на более широкие классы групп, и прежде всего на группы в пространствах размерности n> 1.

В 20 веке расширились связи теории автоморфных функций с другими областями математики, и прежде всего с теорией чисел. Одними из первых приложений к теории чисел были результаты о числе представлений rF(n) целого числа n положительно определённой квадратичной формой F(х, х), где х ЄZ^s (т. е. о числе решений уравнения F(х, х) = n). Оказалось, что ряд

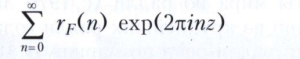
представляет собой автоморфную форму относительно некоторой подгруппы группы SL(2, Z). Отсюда вытекают нетривиальные оценки для r_F(n) при больших n, а в некоторых случаях и явные формулы.

Дальнейшее развитие арифметической теории квадратичных форм, как определённых, так и неопределённых, связано с работами немецкого учёного К. Зигеля, где изучалась их связь с автоморфными формами от нескольких переменных.

Другое направление теории автоморфных функций берёт своё начало в работах М. Эйхлера и Г. Шимуры о дзета-функциях модулярных кривых. Если f(z) - автоморфная форма относительно модулярной группы, то она инвариантна относительно сдвига z→z + 1 и её можно разложить в ряд Фурье

Заменяя ехр(2π?nz) на n^-5 и умножая весь ряд на (2π)^-s Г(s), где Γ(s) - гамма-функция, получают функцию ζ_f(s)комплексной переменной s - преобразование Меллина функции f(z). Оказывается, что функция ζ_f(s)удовлетворяет функциональному уравнению

где m чётно. Развитие этого круга идей привело к гипотезе Таниямы - Вейля, связывающей дзета-функции эллиптических кривых и модулярные формы. Эта гипотеза была доказана английским учёным Э. Уайлзом в 1994 году, что явилось основным средством для доказательства великой теоремы Ферма.

Далеко идущее обобщение этой конструкции было предложено в так называемой программе Ленглендса, связывающей представления групп Галуа полей алгебраических чисел и автоморфные формы на группах аделей. Помимо работ Р. Ленглендса к этой области относятся работы А. Вейля, И. М. Гельфанда, И. И. Пятецкого-Шапиро и др.

Лит.: Форд Р. Автоморфные функции. М.; Л., 1936; Зигель К.Л. Автоморфные функции нескольких комплексных переменных. М., 1954; Ганнинг Р. К. Лекции о модулярных формах // Математика. 1964. Т. 8. № 6; Гельфанд И. М., Граев М. И., Пятецкий-Шапиро И. И. Теория представлений и автоморфные функции. М., 1966; Шимура Г. Введение в арифметическую теорию автоморфных функций. М., 1973; Жаке Э., Ленглендс Р. Автоморфные формы на GL(2). М., 1973; Андрианов А.Н., Журавлев В. Г. Модулярные формы и операторы Гекке. М., 1990.