Кодирование

КОДИРОВАНИЕ, операция отождествления символов или групп символов одного кода с символами или группами символов другого кода. Необходимость кодирования возникает, прежде всего, из потребности приспособить форму сообщения к данному каналу связи или какому-либо другому устройству, предназначенному для преобразования или хранения информации. Так, с помощью телеграфных кодов сообщения, представленные в виде последовательности букв и цифр, преобразуются в определённые комбинации точек и тире. Другой целью кодирования является защита сообщений от несанкционированного доступа (смотри Криптография).

Цель кодирования в информации теории состоит в уменьшении так называемой избыточности сообщений и влияния помех, искажающих сообщения при передаче по каналам связи (смотри Шеннона теорема). Поэтому выбор нового кода стремятся согласовать со статистическими свойствами источника сообщений. В какой-то степени это согласование имеется уже в коде Морзе, в котором чаще встречающиеся буквы обозначаются более короткими комбинациями точек и тире.

Приёмы, применяемые в теории информации для достижения указанного согласования, можно пояснить на примере построения экономных двоичных кодов. Пусть канал связи может передавать только символы 0 и 1, затрачивая на каждый одно и то же время t. Для уменьшения времени передачи (или для увеличения её скорости) целесообразно до передачи кодировать сообщения таким образом, чтобы средняя длина L кодового обозначения была наименьшей. Пусть х₁,х₂,...,х_n обозначают возможные сообщения некоторого источника, а р₁,р₂,...,р_n - соответствующие им вероятности. Тогда, как устанавливается в теории информации, при любом способе кодирования

L ≥ Н, (1)

где H = ∑ⁿ_i=1p_ilog2(1/p_i) - энтропия источника. Равенство в формуле (1) может не достигаться. Однако при любых р₁,р₂,...,р_n существует метод кодирования (метод Шеннона - Фэно), для которого

L ≤ Н+1. (2)

Метод состоит в том, что сообщения располагаются в порядке убывания вероятностей и полученный ряд делится на две части с суммарными вероятностями, по возможности близкими друг к другу. В качестве первого двоичного знака принимают 0 в 1-й части и 1 - во 2-й. Таким же образом делят пополам каждую из частей и выбирают второй двоичный знак и т. д., пока не придут к частям, содержащим только по одному сообщению.

Пример 1. Пусть n = 4 и P₁=⁹/₁₆, p₂ = p₃=³/₁₆, p₄ = ¹/₁₆. Применение метода иллюстрируется таблицей

причём никакой другой код не даёт для L меньшего значения. В то же время H = 1,623. Всё сказанное применимо и к случаю, когда алфавит нового кода содержит не две, как предполагалось выше, а m > 2 букв. При этом величина Н в формулах (1) и (2) должна быть заменена величиной Н/log₂m.

Задача о сжатии записи сообщений в данном алфавите (т. е. задача об уменьшении избыточности) может быть решена на основе метода Шеннона-Фэно. Если сообщения представлены последовательностями длины N букв из m-буквенного алфавита, то их средняя длина L_N после кодирования всегда удовлетворяет неравенству

где Н - энтропия источника на букву. Кроме того, при сколь угодно малом ε > 0 можно добиться выполнения при всех достаточно больших N неравенства

С этой целью используют кодирование блоками: по данному ε выбирают достаточно большое натуральное число s и делят каждое сообщение на равные части - блоки, содержащие по s букв. Затем эти блоки кодируют методом Шеннона-Фэно в тот же алфавит. Тогда при достаточно больших N будет выполнено неравенство (3). Справедливость этого утверждения легче всего понять, рассматривая случай, когда источником является последовательность независимых символов 0 и 1, появляющихся соответственно с вероятностями р и q, 0 < р < 1. Энтропия на блок равна s-кратной энтропии на одну букву, т. е. равна sH = s(plog₂1/р + qlog₂1 /q). Кодовое обозначение блока требует в среднем не более sH + 1 двоичных знаков. Поэтому для сообщения, состоящего из N букв,

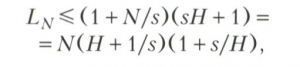
что при достаточно больших s и N/s приводит к неравенству (3). При таком кодировании энтропия на букву приближается к своему максимальному значению - единице, а избыточность - к нулю.

Пример 2. Пусть источником сообщений является последовательность независимых знаков 0 и 1, в которой вероятность появления нуля равна р=3/4, а единицы - q = 1/4. Здесь энтропия Н на букву равна 0,811, а избыточность - 0,189. Наименьшие блоки (s = 2), то есть 00, 01, 10, 11, имеют соответственно вероятности р² = ⁹/₁₆, pq = ³/₁₆, qp = ³/₁₆, q = ¹/₁₆. Применение метода Шеннона-Фэно приводит к следующему правилу кодирования: 00 → 0,01 → 10, 10 → 110, 11 → 111. При этом, например, сообщение 00111000... примет вид 01111100.... На каждую букву сообщения в прежней форме приходится в среднем 27/32 = 0,844 буквы в новой форме (при нижней границе коэффициента сжатия, равной Н = 0,811). Энтропия на букву в новой последовательности равна 0,811/0,844 = 0,961, а избыточность равна 0,039.

Ю. В. Прохоров.