Дифференциальная геометрия

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ, раздел геометрии, в котором геометрические объекты изучаются методами математического анализа, в первую очередь методами дифференциального исчисления. Важнейшие объекты дифференциальной геометрии - кривые (линии) и поверхности евклидова пространства, а также семейства (непрерывные совокупности) кривых и поверхностей. При этом, в отличие от элементарной и аналитической геометрий, изучающих отдельные кривые и поверхности или специальные классы кривых и поверхностей, дифференциальная геометрия рассматривает преимущественно кривые и поверхности вообще, лишь бы их можно было задавать уравнениями, которые исследуются методами математического анализа. Характерной особенностью дифференциальной геометрии является то, что она исследует, прежде всего, свойства геометрических объектов (кривых, поверхностей и их семейств), которые присущи сколь угодно малым их частям; такие свойства называются дифференциальными.

Первоначально в дифференциальной геометрии изучались дифференциальные свойства геометрических объектов, не изменяющиеся при движениях. Это направление в дифференциальной геометрии называют классическим. К другим направлениям дифференциальной геометрии относятся теории, изучающие как дифференциальные свойства геометрических объектов евклидова пространства, не изменяющиеся при аффинных, проективных и других преобразованиях, так и дифференциальные свойства геометрических объектов в неевклидовых многомерных пространствах (например, в трёхмерном или многомерном пространстве Лобачевского), а также дифференциальные свойства самих неевклидовых пространств. Исследования неевклидовых пространств составляют большой и важный раздел дифференциальной геометрии, имеющий тесные связи с физикой, особенно с теорией относительности.

Отвлечение от специальных свойств геометрических объектов, изучаемых в дифференциальной геометрии, приводит к общему понятию дифференциально-геометрического многообразия, содержащему как частные случаи понятия кривой, поверхности, семейства кривых и поверхностей в евклидовых и неевклидовых пространствах, а также сами эти пространства. Таким образом, дифференциально-геометрическое многообразие является предметом дифференциальной геометрии.

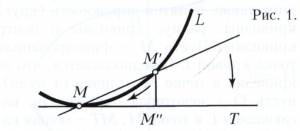
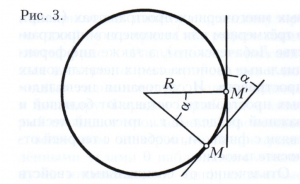
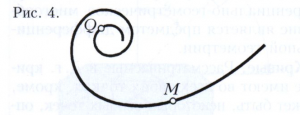
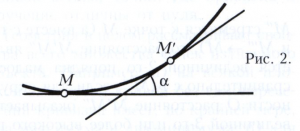Кривые. Рассматриваемые в дифференциальной геометрии кривые имеют во всех своих точках, кроме, может быть, некоторых особых точек, определённую касательную. При обычных в дифференциальной геометрии допущениях достаточной гладкости кривой длина перпендикуляра М’М”» (рисунок  1), опущенного  из  точки  кривой М’ на касательную МТ в точке М, является бесконечно малой величиной, порядок малости которой по сравнению с длиной отрезка ММ" не ниже второго (т. е. отношение М’М”/(ММ”)² остаётся ограниченным, когда точка М’ приближается к М). Мерой отклонения кривой от касательной МТ является кривизна k кривой в точке М, k=2lim М’М”/(ММ”)², где предел берётся при стремлении точки М’ к точке М. Кривизну можно рассматривать также как меру скорости изменения направления кривой. Если обозначить через  α (рис. 2)  угол  между касательными в точках М и М’ и через ∆s длину дуги  ММ’, то k = lim_{∆s →0} α/∆s. При  некоторых условиях кривизне плоской кривой приписывают знак плюс или минус. В частном случае, когда линия - прямая, её направление во всех точках одно и то же, поэтому α = 0 для любого отрезка ММ’ и, значит, k = 0, то есть кривизна прямой во всех точках равна нулю. В другом частном случае, когда линия - окружность, ∆s = αR  (R - радиус  окружности, смотри рисунок 3) и k = lim_∆s→0 α/∆s = 1/R, т. е. кривизна окружности во всех точках одинакова и равна обратной величине радиуса. В случае произвольной линии кривизна в разных точках, вообще  говоря,  различна;  например, на  рисунке 4 кривизна изображённой линии в точке Q больше, чем в точке М.

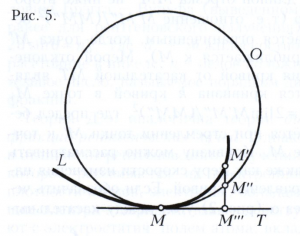
Для характеристики искривлённости кривой вблизи данной точки применяются также понятия окружность (круг) кривизны, радиус кривизны и центр кривизны. Пусть М - фиксированная точка кривой L (предполагается, что её кривизна в точке М отлична от нуля), пусть О - некоторая окружность, касающаяся L в точке М, МТ - общая касательная к L и к окружности О в точке М, М’ и М" - точки, соответственно, на L и на О, имеющие общую проекцию М’’’  на  МТ  (рис. 5). Если  точки  М’  и М" стремятся к точке М (а вместе с тем и М’’’→ М), то расстояние М’М" является величиной 2-го порядка малости сравнительно с ММ’’’если для окружности О расстояние М’М" оказывается величиной 3-го или более высокого порядка (т. е. эта окружность, как говорят, имеет касание 2-го порядка), то она называется соприкасающейся окружностью кривой L в точке М.

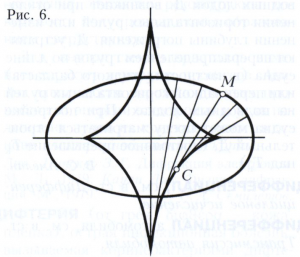
Если в точке М кривизна равна нулю, то соприкасающаяся окружность вырождается в прямую. Таким образом, малую дугу произвольной кривой можно считать дугой окружности, а именно - соприкасающейся окружности в некоторой её точке, если учитывать величины 1-го и 2-го порядков малости (сравнительно с размерами дуги). Кривизна произвольной кривой в данной точке совпадает с кривизной соприкасающейся окружности в той же точке. Поэтому соприкасающуюся окружность называют также окружностью (кругом) кривизны, а её центр и радиус - центром и радиусом кривизны кривой в данной точке. Прямая, соединяющая центр кривизны с точкой М, перпендикулярна касательной, в случае плоской кривой она называется нормалью, а в случае пространственной кривой - главной нормалью. Кривизна k и радиус кривизны р в любой точке кривой связаны соотношением k = 1/р. Множество центров кривизны плоской кривой называется её эволютой. Сама кривая по отношению к своей эволюте называется эвольвентой. Нормаль эвольвенты касается эволюты в центре кривизны.  На  рисунке 6  изображена эволюта эллипса; точка С является центром кривизны эллипса в точке М.

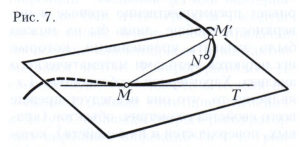
Плоскость, в которой расположена соприкасающаяся в точке М окружность, называется соприкасающейся плоскостью в точке М. Эту плоскость можно определить непосредственно как плоскость, для которой длина перпендикуляра М’N  (рис. 7), опущенного из  точки М’, является бесконечно малой не ниже  3-го порядка по сравнению с MM’ (для произвольной плоскости, проходящей через М, длина М’N, вообще говоря, будет бесконечно малой 1-го порядка, а для плоскости, проходящей через касательную МТ, вообще говоря, 2-го порядка). Соприкасающаяся плоскость есть не что иное, как плоскость, проходящая через касательную и главную нормаль. В точке М с кривизной, равной нулю, соприкасающаяся плоскость не определена.

При изучении пространственных кривых, кроме кривизны, вводится понятие кручения. Если кривая не лежит целиком в одной плоскости, то её соприкасающиеся плоскости при переходе от точки к точке меняются; чем резче происходит это изменение, тем большим кручением обладает кривая. Численно кручение определяется следующим образом. Пусть переменная точка перемещается по кривой из М в М’; соприкасающаяся плоскость в переменной точке меняет угол своего наклона к соприкасающейся плоскости в точке М (начиная от нуля) и в точке М’ располагается к ней под некоторым углом β (если смещение точки мало, то β - малый острый угол). Углу β приписывается знак плюс, если наблюдатель, глядя из М в М’, будет видеть вращение переменной соприкасающейся плоскости по часовой стрелке; в противном случае углу β приписывается знак минус. Отношение β/Δs, где ∆s - длина дуги ММ’, принимается в качестве меры кручения кривой в среднем на участке ММ’. Предел этого отношения при ∆s → 0 называется кручением ς в точке М. В частном случае, когда кривая является плоской, её кручение во всех точках равно нулю; обратно, если кручение во всех точках равно нулю, то кривая целиком лежит в одной плоскости - общей соприкасающейся плоскости для всех её точек.

Кривизна и кручение - величины, характеризующие кривую, именно: если между точками двух кривых установлено соответствие так, что соответствующие дуги этих кривых имеют одинаковые длины, и если в соответствующих точках эти кривые имеют равные кривизны и равные кручения, то они одинаковы по форме, т. е. могут быть совмещены при помощи движения. Например, все кривые, вдоль которых кривизна постоянна и равна 1/α, а кручение равно нулю, суть окружности радиуса α. Произвольно задав непрерывные функции k(s) ≥ 0 и ς(s), можно найти кривую с этой заданной зависимостью кривизны k и кручения ς от s, где s - длина дуги кривой, измеряемой от некоторой фиксированной точки этой кривой.

Основные понятия дифференциальной геометрии широко используются в механике. Можно отметить, что скорость движущейся точки направлена по касательной к её траектории, вектор ускорения лежит в соприкасающейся плоскости. Если движение по кривой равномерно, то при данной скорости ускорение пропорционально кривизне траектории и направлено к центру кривизны. Поэтому, например, при установлении предельной скорости движения поезда на криволинейном участке пути необходимо учитывать кривизну участка, чтобы не допустить ускорения, при котором инерционные силы превысят границы безопасности; переход от прямого участка к криволинейному должен быть осуществлён таким образом, чтобы кривизна возрастала от нуля не слишком быстро, так как в противном случае неизбежны возникновения больших инерционных сил.

Дифференциальная  геометрия даёт общие способы для нахождения касательной, кривизны, кручения кривой. При этом кривая предполагается заданной уравнениями в какой-либо системе координат, чаще всего параметрическими уравнениями в прямоугольных координатах (1)

здесь u - независимая переменная (называемая параметром), изменяющаяся в некотором конечном или бесконечном интервале; φ(u), ψ(u), χ(u) - заданные функции; х, у, z - прямоугольные координаты некоторой точки М. При изменении u меняются величины х, у, z, что означает перемещение точки М. Траектория точки М представляет собой кривую, заданную уравнениями (1). Например, уравнения х = а cos u , у = а sin u, z = bu, а > 0, b ≠ 0, определяют винтовую линию: при возрастании u точка М вращается вокруг оси Oz и одновременно перемещается  вдоль  этой  оси.

Правые части уравнений (1) можно рассматривать как проекции на оси координат радиус-вектора r точки М, что записывается так:

Вектор с проекциями φ’(u), ψ’(u), χ’(u) называется производной вектора r и обозначается

 

аналогично определяются производные высших порядков:

Вектор r’ лежит на касательной к кривой в точке М. Поэтому если r’≠0, то касательная определяется точкой М и вектором r’. Вектор r" лежит в соприкасающейся плоскости. Поэтому соприкасающаяся плоскость определяется точкой М и векторами r’ и r" (если эти векторы неколлинеарны). Кривизна и кручение вычисляются по формулам (2)

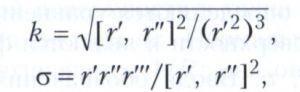
где [r’, r" ] - векторное, а r’r"r’’’ смешанное произведения. При этом предполагается, что система координатных осей имеет правую ориентацию. Кривизна и кручение суть дифференциальные инварианты относительно изменения параметра. Это означает, что они выражаются через дифференциалы вектора r и параметра u и их выражения не изменяются (т. е. инвариантны) при переходе к новому параметру v по формуле u = u(v).

Для применения формул (2) необходимо, чтобы правые части уравнений (1), определяющих кривую, имели производные, по крайней мере, до 3-го порядка. Это условие относительно рассматриваемых кривых в дифференциальной геометрии обычно предполагается выполненным. Кроме того, как правило, предполагается, что r’≠0. В каждой точке, где оба указанных условия выполнены, кривая имеет касательную и вблизи такой точки простирается вдоль касательной в обе стороны. Вблизи точки, где r’=0, кривая может иметь иное строение, такая точка называется  нерегулярной  или  особой.

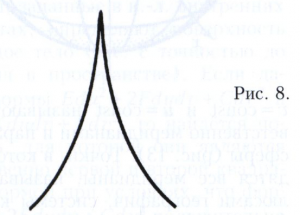
Пример особой точки (так называемой точки возврата) смотри на рисунке 8. Смотри также Особая точка кривой.

Если параметр u совпадает с длиной дуги s, пройденной точкой М по данной кривой, считая от некоторой выбранной начальной точки, то dr/du = dr/ds = t - единичный вектор касательной. Вектор d²r/ds² перпендикулярен вектору t и направлен по главной нормали. Единичный вектор, направленный так же, как d²r/ds², называют единичным вектором главной нормали; его обычно обозначают через n. Нормаль, перпендикулярная к соприкасающейся плоскости, называется бинормалью; вектор b, равный векторному произведению t на n (т. е. b=[t, n]) и направленный перпендикулярно к соприкасающейся плоскости, называется единичным вектором бинормали. Плоскость, проходящая через точку М и векторы n, b, содержит все нормали в точке М и называется нормальной плоскостью в этой точке; плоскость, проходящая через векторы t, b, называется спрямляющей.

Векторы t, n, b составляют так называемый основной триэдр кривой в точке М; они являются функциями того же параметра, который определяет положение точки М. В частности, если в качестве параметра выбрана длина дуги s, то t, n, b будут функциями s. Производные t, n, b  по  s выражаются формулами Френе:

которые широко используются в дифференциальной геометрии и теоретической механике.

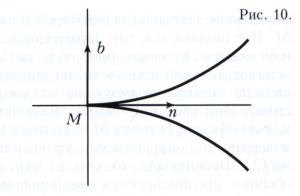
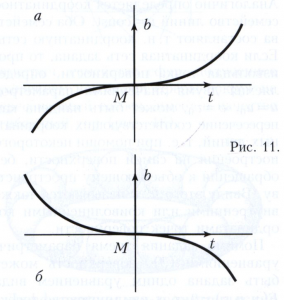
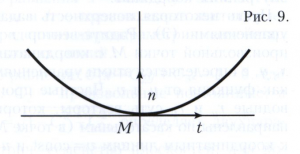Если кривизна и кручение кривой в некоторой  её  точке отличны от нуля, то, зная их, можно сделать определённые заключения о форме кривой в достаточно малой окрестности точки М. Именно, её проекция на соприкасающуюся плоскость в точке М является выпуклой и расположена по ту сторону от касательной, в которую направлен вектор n (рис. 9); проекция на нормальную плоскость имеет точку возврата (рис. 10); проекция на спрямляющую плоскость - точку перегиба, причём в случае ς > 0 кривая расположена так, как на рисунке 11, а, в  случае  ς<0 - как на рисунке 11, б.

В дифференциальной геометрии, в частности в теории кривых, различают два рода теорем: теоремы геометрии в малом и теоремы геометрии в целом. В геометрии в малом утверждения относятся не ко всему множеству точек изучаемого объекта (например, кривой), а только к части этого множества, принадлежащей какой-либо окрестности некоторой его точки. К геометрии в малом относится, например, исследование формы кривой вблизи точки, где кривизна и кручение отличны от нуля.

Геометрия в целом рассматривает свойства всего множества точек изучаемого объекта. Например: а) на всякой плоской замкнутой кривой без самопересечений кривизна имеет, по крайней мере, два максимума и два минимума; б) для любой замкнутой кривой ∮kds ≥ 2π (знак равенства имеет место только для плоских выпуклых кривых, а если кривизна берётся с учётом знака, то - для плоских замкнутых кривых).

Поверхности. Поверхность в дифференциальной геометрии обычно определяется тремя уравнениями (3)

где u, v - независимые переменные, называемые параметрами, а х, у, z - прямоугольные координаты некоторой точки М. Предполагается, что параметры u, v изменяются в некоторой области D вспомогательной плоскости, на которой введена система прямоугольных координат. При всех возможных значениях u, v из области D точка М находится на поверхности, определяемой уравнениями (3). Функции φ(u, v), ψ(u, v), χ(u, v) обычно предполагаются непрерывными и обладающими частными производными, по крайней мере, до 3-го порядка при всех рассматриваемых значениях u, v. Для каждой пары значений u, v уравнения (3) устанавливают определённое положение точки М на поверхности. Если зафиксирована только величина v, то при изменении u точка М описывает на поверхности некоторую линию, называемую координатной; разным значениям v соответствуют различные (вообще говоря) координатные линии; все вместе они составляют координатное семейство линий v = const. Аналогично определяется координатное семейство линий u = const. Оба семейства составляют так называемую координатную сеть. Если координатная сеть задана, то произвольная точка поверхности, определяемая двумя значениями параметров u = u₀, v = v₀, может быть найдена как пересечение соответствующих координатных линий, т. е. при помощи некоторого построения на самой поверхности, без обращения к объемлющему пространству. Ввиду этого u, v называются также внутренними или криволинейными координатами точек поверхности.

Помимо задания тремя параметрическими уравнениями (3), поверхность может быть задана одним уравнением вида F(х, у, z) = 0, т. е. как множество точек, координаты которых удовлетворяют этому уравнению. Если параметрические уравнения поверхности заданы, то исключение параметров u, v из этих уравнений приводит к соотношению между х, у, z указанного вида.

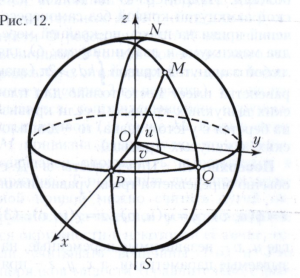
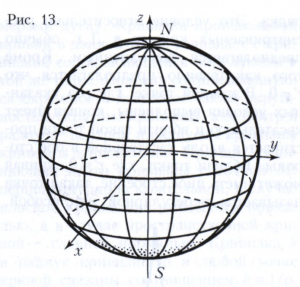
Например, уравнения х = а sin u  cos υ, у = а sin u sin v, z = а cos u, а > 0, определяют сферу радиуса а с центром в начале координат. В данном случае u, v называются географическими координатами точек сферы (если u, v - внутренние координаты точки М, то u есть угол MOQ, а  v  есть  угол  POQ;  рисунок 12).  Линии u = const и v = const называются соответственно меридианами и параллелями сферы (рис. 13). Точки, в которых сходятся все меридианы, называются полюсами географической системы координат (на рисунке 13 это точки N и S). Исключение параметров u, v из данных трёх параметрических уравнений сферы приводит к уравнению х² + у² + z² = а².

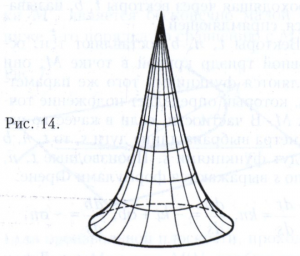
Дифференциальная  геометрия в первую очередь изучает так называемые регулярные, или обыкновенные, точки поверхности. Точка поверхности называется регулярной, если в некоторой её окрестности можно ввести внутренние координаты так, что через каждую точку этой окрестности проходят одна линия семейства u = const и одна линия семейства v = const, причём направления этих линий различны. При этих условиях и сама координатная система называется регулярной. Например, географическая система координат на сфере регулярна всюду, за исключением полюсов N и S; однако и точки N и S - регулярные точки сферы, т.к. на сфере можно ввести другую географическую систему координат (с новыми полюсами), которая в этих точках будет регулярной. Точка поверхности, не являющаяся регулярной, называется особой (на  рисунке 14 изображена поверхность с особой точкой). В дальнейшем рассматриваются только регулярные точки и регулярные системы внутренних координат.

Пусть некоторая поверхность задана уравнениями (3). Радиус-вектор r её произвольной точки М с координатами х, у, z определяется этими уравнениями как функция от u и v. Частные производные r_u и r_v суть векторы, которые направлены по касательным (в точке М) к координатным линиям u = const и v =  const, проходящим через М. В случае регулярной точки и регулярной системы координат векторы r_u и r_v неколлинеарны. Поэтому существует одна плоскость, которая проходит через точку М и содержит векторы r_u и r_v. Эта плоскость содержит касательную к каждой линии, которая проходит на поверхности через точку М. Она называется касательной плоскостью к поверхности в точке М. Прямая, которая проходит через точку М перпендикулярно к касательной плоскости (в точке М), называется нормалью к поверхности в точке М. Направление нормали определяется векторным произведением [r_u и r_v].

Пусть  даны  уравнения (4)

тогда вектор r является функцией от t с (промежуточными) аргументами u, v. При изменении t конец вектора r будет описывать на данной поверхности некоторую линию; уравнения (4) называются внутренними уравнениями этой линии. Одной из общих задач теории поверхностей является задача исследования линий на поверхности по их внутренним уравнениям. В первую очередь возникает вопрос об измерении линии, т. е. о вычислении длины любой её дуги.

Пусть s - длина дуги линии на поверхности, измеренная от некоторой её фиксированной точки до произвольной точки М с внутренними координатами u, v. Т. к. u = φ(t), v = ψ(t), то s является функцией параметра t; дифференциал этой функции определяется равенством (5)

Правая часть этого равенства есть скалярный квадрат вектора dr. Т.к. dr = r_udu + r_vdv, то (6)

Здесь du и dv определяются из уравнения данной линии, а именно: du = φ’(t)dt, dv = ψ’(t)dt.   Напротив,  коэффициенты r²_u , r_ur_v и r²_v   не зависят от каких бы то ни было линий, проводимых на поверхности, они определяются уравнениями (3) самой поверхности и являются функциями от u, v. Вводя обозначения r²_u  = Е, r_ur_v = F, v²_u  = G, равенство (6) можно переписать в виде (7)

Выражение в правой части называется первой  квадратичной  формой. Если  Е, F, G известны, то длина произвольной дуги линии (4), соответствующей изменению t в отрезке [t₁,t₂], может быть вычислена по формуле

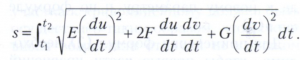
Квадратичная форма (7) позволяет вычислять длины дуг линий на данной поверхности, поэтому её называют метрической формой поверхности. Вместе с тем первая квадратичная форма определяет внутреннюю геометрию поверхности, т. е. совокупность фактов, которые могут быть получены при помощи измерений, производимых на самой поверхности, без обращения к объемлющему пространству. Внутренняя геометрия поверхностей является широким обобщением планиметрии. Роль прямых во внутренней геометрии произвольной поверхности играют геодезические линии. Две поверхности имеют одинаковую внутреннюю геометрию, если их можно взаимно однозначно отобразить одну на другую так, что геодезические линии перейдут в геодезические и длины их останутся неизменными. Такие поверхности называются изометричными.

Непрерывная деформация поверхности, при которой её внутренняя геометрия остаётся неизменной, называется изгибанием поверхности. Если поверхность физически реализована из гибкого нерастяжимого материала, то, деформируя её так, чтобы не возникало складок или разрывов, получают изгибание этой поверхности. Исследование изгибаний имеет важное значение для теории упругих оболочек.

Дифференциальная  геометрия не ограничивается изучением только внутренних свойств поверхности. Изучение поверхности как пространственной фигуры основано на рассмотрении кривизны лежащих на поверхности линий. Пусть М - произвольная точка поверхности, определяемой уравнениями (3), N - единичный вектор нормали в точке М (обычно вектор N предполагается направленным по нормали в ту же сторону, в какую направлено векторное произведение [r_u, r_v]). Если провести плоскость через нормаль в точке М в направлении данного вектора dr = r_udu + r_vdv, то она пересечёт поверхность по некоторой линии. Кривизна этой линии в точке М, взятая со знаком плюс, если направление вогнутости линии совпадает с направлением вектора N, и со знаком минус в противоположном случае, называется нормальной кривизной поверхности в точке М в направлении вектора dr. Нормальная кривизна обозначается 1/R; она определяется формулой

Где

а ds² определяется по формуле (7). Квадратичная  дифференциальная  форма

называется второй квадратичной формой поверхности. Нормальная кривизна поверхности (в некоторой её точке М) зависит от направления вектора dr. Те направления, в которых нормальная кривизна принимает экстремальное значение, называются главными направлениями поверхности в точке М. Направления, в которых нормальная кривизна обращается в нуль, называются асимптотическими. О зависимости вида поверхностей вблизи данной точки от вида второй квадратичной формы смотри в статье Поверхностей теория.

Методы исследования поверхностей в малом хорошо разработаны. В основном они базируются на следующем положении: две квадратичные формы поверхности, заданные в каких-либо внутренних координатах, определяют поверхность как твёрдое тело (т. е. с точностью до положения в пространстве). Если даны две формы Edu² + 2Fdudv + Cdv² и Hdu² + 2Kdudv + Ldv², то найдётся поверхность, для которой они являются соответственно первой и второй квадратичной формой при условиях, что форма Edu² + 2Fdudv + Cdv² положительна и функции Н, К, L удовлетворяют некоторой системе трёх уравнений, одно из которых, найденное К. Гауссом (1827), является алгебраическим, а два других уравнения, найденные К. М. Петерсоном (1853), суть линейные дифференциальные уравнения с частными производными 1-го порядка. Уравнения Гаусса - Петерсона играют фундаментальную роль в теории поверхностей.

Геометрия поверхностей в целом устанавливает свойства поверхностей по их дифференциальным свойствам в каждой точке, она богата глубокими результатами, но менее развита, чем геометрия в малом.

Семейства  кривых  и поверхностей.

В дифференциальной геометрии часто приходится иметь дело не с отдельной кривой и поверхностью, а с бесконечными семействами кривых или поверхностей. Пусть даны уравнения, которые содержат координаты х, у, z и произвольные постоянные С₁,С₂, ..., С_n, причём каждый раз, когда эти постоянные получают какие-либо численные значения, данные уравнения определяют некоторую кривую (или поверхность). Множество всех кривых (или поверхностей), которые определяются данными уравнениями при всех возможных численных значениях  С₁,С₂, ..., С_n,  называется n-параметрическим семейством кривых (или поверхностей). При этом предполагается, что то же самое множество не может быть определено уравнениями с меньшим  числом  произвольных постоянных.

Примеры. Уравнение  xcosα + ysinα – 1 = 0,  где α - произвольная постоянная, определяет однопараметрическое семейство прямых, для которых расстояние до начала координат равно единице.

Уравнения х = acost, у = sint, z = bt, где а и b - произвольные постоянные, определяют двухпараметрическое семейство винтовых линий.

Уравнение C₁x + C₂y + C₃z – 1 = 0, где С₁, С₂  -  произвольные   постоянные,  а C₃ = √(1-C₁²-C₂²), определяет двухпараметрическое семейство плоскостей, для которых расстояние до начала координат равно единице.

При изучении однопараметрических семейств кривых, а также одно- и двухпараметрических семейств поверхностей важную роль играет понятие огибающей. Огибающей однопараметрического семейства кривых называется кривая, которая в каждой своей точке касается какой-либо кривой семейства.

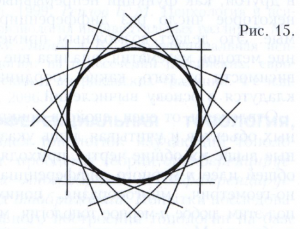
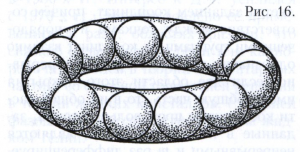
Например, семейство прямых на плоскости, отстоящих от данной точки на расстоянии, равном а, имеет в качестве огибающей окружность радиуса а с центром  в  данной точке (рис. 15); однопараметрическое семейство сфер, полученное вращением некоторой сферы вокруг не пересекающей её оси, имеет в качестве огибающей тор (рис. 16).

Дифференциально-геометрические многообразия. В различных разделах дифференциальной геометрии и в её применениях рассматриваются разнообразные объекты. При всём разнообразии этих объектов они обладают некоторыми общими чертами. Прежде всего, они суть множества, для которых определено понятие близости элементов (линии и поверхности суть множества точек, семейства суть множества линий и поверхностей). Далее, они являются многомерными топологическими многообразиями, т. е. вблизи каждого своего элемента имеют то же топологическое строение, что и евклидово пространство некоторой размерности (вблизи некоторых элементов множество может иметь более сложное топологическое строение, но такие элементы исключаются из рассмотрения как особые; например, конус вблизи каждой своей обыкновенной точки имеет такое же строение, как евклидова плоскость, вершина же конуса является особой точкой). Наконец, множества, изучаемые в дифференциальной геометрии, рассматриваются всегда вместе с заданными координатами элементов; при этом число координат для каждого элемента равно размерности множества и координаты непрерывно зависят от элемента, т. е. при бесконечно малом перемещении элемента его координаты изменяются бесконечно мало. Таковы, например, декартовы координаты на плоскости. Однако во многих случаях, например на сфере, введение таких координат на всём множестве невозможно, но в этих случаях для множеств, рассматриваемых в дифференциальной геометрии, можно указать конечную или счётную систему областей, совместно покрывающих множество, в каждой из которых могут быть введены координаты с соблюдением указанных условий. При этом в общей части каждой пары таких областей координаты произвольного элемента, введённые в любой из них, выражаются через координаты, введённые в другой, как функции непрерывные и некоторое число раз дифференцируемые. Это делает возможным применение методов математического анализа вне зависимости от того, какие координаты кладутся в основу вычислений.

Отвлекаясь от специальных свойств конкретных объектов и учитывая лишь указанные выше их общие черты, приходят к общей идее n-мерного дифференциально-геометрического многообразия, понимая под этим любое n-мерное топологическое многообразие М при следующих условиях: многообразие М покрыто конечным или счётным множеством областей, в каждой из которых введена координатная система так, что каждая точка определяется заданием координат, причём соответствие между точками и упорядоченными группами их координат взаимно однозначно и в обе стороны непрерывно; если две области этого покрытия имеют общую часть, то в их общей части координаты произвольной точки, заданные в какой-либо из областей, являются непрерывными и m раз дифференцируемыми или аналитическими функциями координат, заданных в другой области, в этом случае многообразие называется m раз дифференцируемым или аналитическим соответственно. Если то же самое топологическое многообразие покрыто новым множеством областей и в каждой из них введена координатная система с соблюдением тех же условий, то считают, что новый способ введения координат приводит к тому же самому дифференциально-геометрическому многообразию, если в каждой общей части двух областей старого и нового покрытия координаты, заданные в какой-либо одной из этих областей, являются непрерывными и m раз дифференцируемыми или аналитическими функциями координат, заданных в другой области. Согласно этому определению, линии суть одномерные дифференциально-геометрического многообразия, поверхности - двумерные, обычное евклидово пространство представляет собой пример трёхмерного дифференциально-геометрического многообразия. Элементы многообразия принято называть точками, однако они могут быть объектами любой природы.

Примеры. Множество, элементами которого являются все прямые обычного евклидова пространства, представляет собой четырёхмерное дифференциально-геометрическое многообразие. Если в декартовых координатах прямая задана уравнениями z = ax + b, z = cy + d, то числа (а, b, с, d) можно рассматривать в качестве координат этой прямой. Область, в которой определена такая координатная система, есть множество всех прямых пространства, за исключением тех, которые параллельны плоскости xOz или плоскости yOz.

Множество, элементами которого являются всевозможные положения твёрдого тела в обычном евклидовом пространстве, представляет собой шестимерное дифференциально-геометрическое многообразие. Оно шестимерно потому, что положение твёрдого тела определяется шестью числами, в качестве которых, например, можно взять три декартовы координаты какой-либо его точки и три эйлеровых угла какой-либо жёстко связанной с телом прямоугольной системы координат.

Множество, элементами которого являются всевозможные положения механической системы n свободных точек, также представляет собой дифференциально-геометрическое многообразие. Размерность его равна 3n, так как положение такой системы определяется заданием 3n координат этих точек. Вообще, механическая система, имеющая k степеней свободы, представляет собой дифференциально-геометрическое многообразие размерности k.

Из приведённых примеров можно видеть, что общее понятие дифференциально-геометрического многообразия охватывает различные конкретные множества, поэтому изучение дифференциально-геометрических многообразий важно для многих областей математики и смежных с ней дисциплин. Важнейшие результаты, связанные с дифференциально-геометрическими многообразиями, получены в римановой  геометрии.

Исторический очерк. Отдельные понятия дифференциальной геометрии (круг кривизны, эволюта, огибающая, геодезическая линия) встречаются уже во 2-й половине 17 века в трудах И. Ньютона, Г. В. Лейбница, Х. Гюйгенса, Я. и И. Бернулли. К концу 18 века работами Л. Эйлера и Г. Монжа были заложены основы теории поверхностей. Л. Эйлер впервые пользовался криволинейными координатами, установил формулу, выражающую нормальную кривизну поверхности, ввёл понятие наложимости поверхностей и рассмотрел поверхности, наложимые на плоскость. Г. Монжу принадлежат понятия линий кривизны и асимптотических линий поверхности. К дифференциальной геометрии относится сочинение Г. Монжа «О земляных выемках и насыпях» (1781), в котором он использовал свои инженерные работы по фортификации. Наиболее известна его монография «Приложение анализа к геометрии» (1795, русский перевод 1936).

Особое значение для дифференциальной геометрии имели работы К. Гаусса, источником которых были задачи геодезии и картографии. Главное сочинение К. Гаусса в этой области - «Общие исследования о кривых поверхностях» (1827). В нём вводятся обе квадратичные формы поверхности и доказывается теорема об инвариантности полной кривизны относительно изометричных преобразований. Принципиальное значение этой работы заключается в том, что в ней появилось понятие внутренней геометрии поверхности. Построение основ классической теории поверхностей завершено К. М. Петерсоном, который в 1853 году дал полную систему уравнений этой теории. Во 2-й половине 19 века множество глубоких и общих результатов по классической теории поверхностей было получено Ф. Миндингом, Ж. Лиувиллем, Э. Бельтрами, Ж. Г. Дарбу и др. В этот период детально исследована внутренняя геометрия поверхности, получены результаты о наложимости поверхностей и основной теоремы об изгибаниях. Одновременно шло исследование важнейших частных классов поверхностей; как правило, эта проблематика находилась в тесной связи с теорией интегрирования дифференциальных уравнений. Обзор результатов, полученных во 2-й половине 19 века, содержится в четырёхтомном трактате Ж. Г. Дарбу «Лекции по общей теории поверхностей» (1887-1896). Среди специальных исследований по теории поверхностей наиболее известны работы К. М. Петерсона, которому принадлежит понятие так называемого изгибания поверхности на главном основании. Большой вклад в проблему, связанную с изгибанием на главном основании, внёс Н. Н. Лузин (1938-39). Российским математиком Д. Ф. Егоровым развита теория так называемых потенциальных поверхностей, интересных с точки зрения механики (1901).

С конца 19 века, в значительной степени в связи с «Эрлангенской программой» Ф. Клейна (1872), в дифференциальной геометрии всё большее место занимают исследования дифференциальных инвариантов различных групп преобразований (аффинных преобразований, проективных преобразований, конформных преобразований).

Теоретико-групповые обобщения классических разделов дифференциальной геометрии способствовали развитию современного понятия геометрического пространства, при этом главными были исследования, связанные с работами Н. И. Лобачевского. Открытие Лобачевского геометрии явилось началом обобщений понятия пространства в том направлении, которое наиболее важно для естествознания. Здесь значительная роль принадлежит Б. Риману; в его лекции «О гипотезах, лежащих в основании геометрии» (1854) даны основы теории пространств, называемых римановыми. Дальнейшее развитие теории римановых пространств соединилось с развитием тензорного анализа, идеи которого были подготовлены работами Г. Ламе (1859), Э. Бельтрами (1868), Э. Кристоффеля (1869) и окончательно сформированы в работах итальянского математика Г. Риччи-Курбастро (1884-1888). Теория римановых пространств и тензорный анализ с начала возникновения находились в тесной связи с механикой  и  математической физикой, позднее они стали основным математическим аппаратом общей теории относительности. В свою очередь, появление общей теории относительности (1915) стимулировало бурное развитие тензорного анализа, теории римановых пространств и их обобщений. В 1917 году Т. Леви-Чивита и независимо от него нидерландский математик Я. Схоутен (1918) определили понятие параллельного переноса вектора в римановом пространстве; в 1918 Схоутен и Г. Вейль обобщили понятие риманова пространства на случай так называемых пространств аффинной и конформной связности. Потребность такого обобщения была вызвана попытками построения единой теории гравитационного и электромагнитного поля. В работах Э. Картана (1922-24) идеи обобщения внутренней геометрии поверхности соединились с теоретико-групповым направлением.

Большие достижения в дифференциальной геометрии относятся к области проблем геометрии в целом. Важные результаты были получены Л. А. Люстерником и Л. Г. Шнирельманом, которые доказали (1930), что на каждой поверхности, гомеоморфной сфере, имеется не менее трёх замкнутых геодезических линий без кратных точек. Проблема о числе таких геодезических линий была поставлена А. Пуанкаре в 1908 году. Немецкому математику С. Э. Кон-Фоссену принадлежат результаты по исследованию поведения геодезических линий на двумерных полных римановых многообразиях, гомеоморфных плоскости (1935-36).

Принципиально новые результаты в теории выпуклых поверхностей были получены А. Д. Александровым, который предложил новый метод исследования выпуклых поверхностей, основанный на их приближении выпуклыми многогранниками (1948). А. В. Погорелову принадлежит построение полной теории выпуклых поверхностей (1969). К качественным вопросам теории поверхностей относятся работы Н. В. Ефимова (1948-49).

Лит.: Стройк Д. Очерк истории дифференциальной геометрии до XX столетия. М.; Л., 1941; Александров А. Д. Внутренняя геометрия выпуклых поверхностей. М.; Л., 1948; Каган В. Ф. Очерки по геометрии. М., 1963; Шуликовский В. И. Классическая дифференциальная геометрия в тензорном изложении. М., 1963; Погорелов А. В. Внешняя геометрия выпуклых поверхностей. М., 1969; он же. Дифференциальная геометрия. 6-е изд. М., 1974; Громол Д., Клингенберг В., Мейер В. Риманова геометрия в целом. М., 1971; Кобаяси Ш., Номидзу К. Основы дифференциальной геометрии. М., 1981. Т. 1-2; Вольф Дж. Пространства постоянной кривизны. М., 1982. По материалам статьи  Н. В. Ефимова из МЭС.